Auto-$\lambda$: Disentangling Dynamic Task Relationships
by Shikun Liu, Stephen James, Andrew J. Davison, & Edward Johns
We present Auto-$\lambda$, a gradient-based meta learning framework which explores continuous, dynamic task relationships via task-specific weightings, and can optimise any choice of combination of tasks through the formulation of a meta-loss. Auto-$\lambda$ unifies multi-task and auxiliary learning problems with a single optimisation framework, and achieves the state-of-the-art performance even when compared to optimisation strategies designed specifically for each problem.
Introduction
Multi-task learning can improve model accuracy, memory efficiency, and inference speed, when compared to training tasks individually. However, it often requires careful selection of which tasks should be trained together, to avoid negative transfer, where irrelevant tasks produce conflicting gradients and complicate the optimisation landscape. As such, without prior knowledge of the underlying relationships between the tasks, multi-task learning can sometimes have worse prediction performance than single-task learning.
We define the relationship between two tasks to mean to what extent these two tasks should be trained together. For example, we say that task $A$ is more related to task $B$ than task $C$, if the performance of task $A$ is higher when training tasks $A$ and $B$ together, compared to when training tasks $A$ and $C$ together.
To determine which tasks should be trained together, we could exhaustively search over all possible task groupings, where tasks in a group are equally weighted but all other tasks are ignored. However, this requires training $2^{|{\bf T}|}-1$ multi-task networks for a set of tasks ${\bf T}$, and the computational cost for this search can be intractable when $|{\bf T}|$ is large. A simple example is visualised below.
* Training Tasks: $A+B+C+D,$ Primary Task: $A$ *
Auto-$\boldsymbol \lambda$
$$\begin{align}
1\text{ - Order}:\, &{\bf 1}\cdot A + 0\cdot B + 0\cdot C + 0\cdot D \\
2\text{ - Order}:\, &{\bf 1}\cdot A + {\bf 1}\cdot B + 0\cdot C + 0\cdot D \\
& {\bf 1}\cdot A + 0\cdot B + {\bf 1}\cdot C + 0\cdot D \\
&{\bf 1}\cdot A + 0\cdot B + 0\cdot C + {\bf 1}\cdot D \\
3\text{ - Order}:\, &{\bf 1}\cdot A + {\bf 1}\cdot B + {\bf 1}\cdot C + 0\cdot D \\
&{\bf 1}\cdot A + {\bf 1}\cdot B + 0\cdot C + {\bf 1}\cdot D \\
&{\bf 1}\cdot A + 0\cdot B + {\bf 1}\cdot C + {\bf 1}\cdot D \\
4\text{ - Order}:\, &{\bf 1}\cdot A + {\bf 1}\cdot B + {\bf 1}\cdot C + {\bf 1}\cdot D \\
\end{align}
$$
$$\lambda_A\cdot A + \lambda_B\cdot B + \lambda_C \cdot C + \lambda_D\cdot D$$
Prior works have developed efficient task grouping frameworks based on heuristics to speed up training, such as using an early stopping approximation and computing a lookahead loss averaged across a few training steps. However, these task grouping strategies are typically bounded by two prominent limitations. Firstly, they are designed to be two-stage methods, requiring a search for the best task structure based on the choice of primary tasks and then re-training of the multi-task network with the best task structure. Secondly, higher-order task relationships for three or more tasks are not directly obtainable due to high computational cost. Instead, higher-order relationships are approximated by small combinations of lower-order relationships, and thus, as the number of training tasks increases, even evaluating these combinations may become prohibitively costly.
In this paper, instead of requiring these expensive searches or approximations, we propose that the relationship between tasks, is dynamic, and based on the current state of the multi-task network during training. We consider that task relationships, parameterised by task-specific weightings, termed $\lambda$, could be inferred within a single optimisation problem, which runs recurrently throughout training, and automatically balances the contributions of all tasks depending on which tasks we are optimising for. In this way, we aim to unify multi-task learning and auxiliary learning into a single framework.
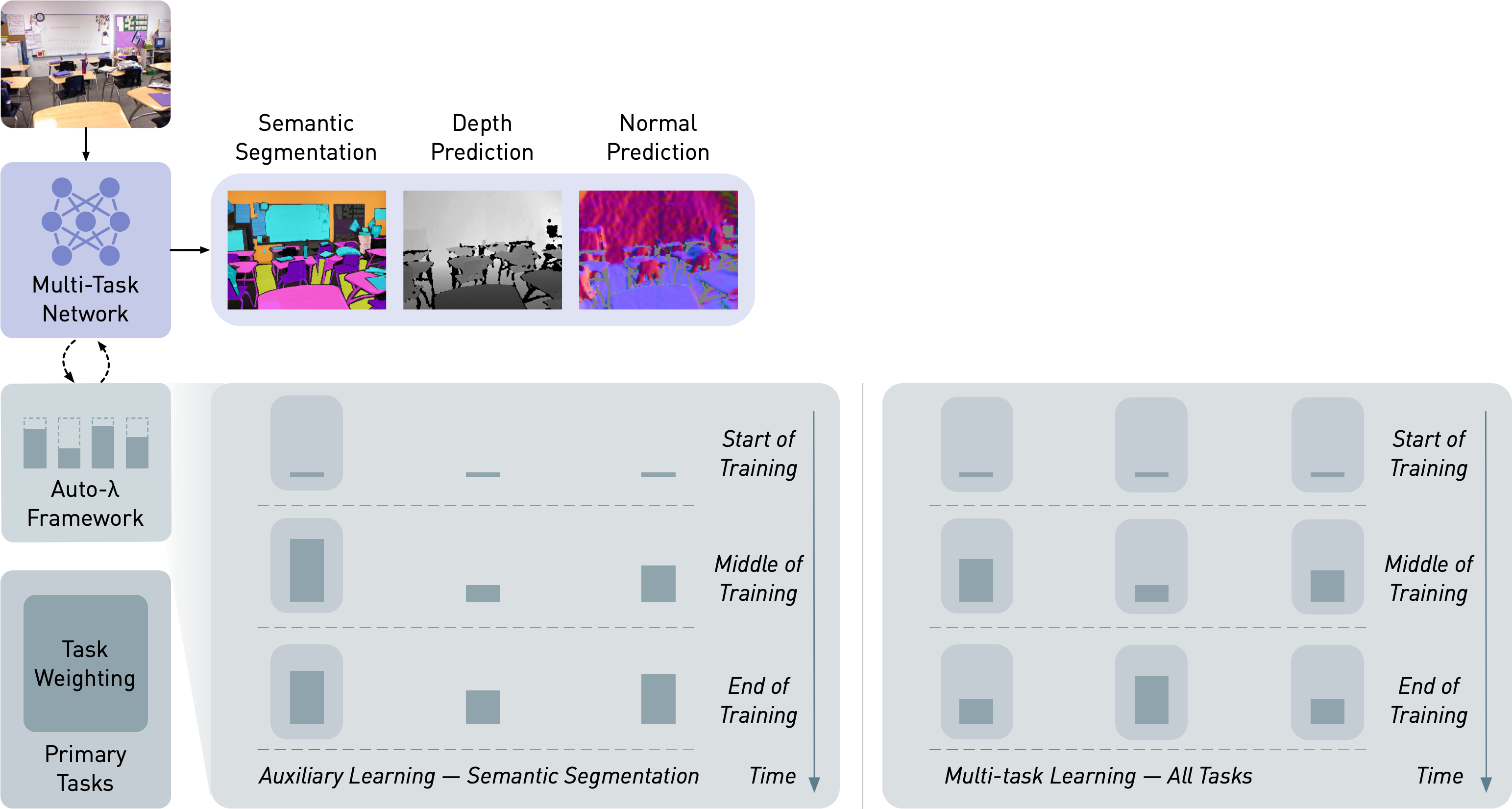
In Auto-$\lambda$, task weightings are dynamically changed along with the multi-task network parameters, in joint optimisation. The task weightings can be updated in both the auxiliary learning setting (one task is the primary task) and the multi-task learning setting (all tasks are the primary tasks). In this example, in the auxiliary learning setting, semantic segmentation is the primary task which we are optimising for. During training, task weightings provide interpretable dynamic task relationships, where high weightings emerge when tasks are strongly related (e.g. normal prediction to segmentation) and low weightings when tasks are weakly related (e.g. depth prediction to segmentation).
Background
Notations
We denote a multi-task network to be $f(\cdot\, ; \boldsymbol \theta)$, with network parameters ${\boldsymbol \theta}$, consisting of task-shared and $K$ task-specific parameters: $\boldsymbol \theta = \left\{\theta_{sh}, \theta_{1:K}\right\}$. Each task is assigned with task-specific weighting $\boldsymbol \lambda=\left\{\lambda_{1:K}\right\}$. We represent a set of task spaces by a pair of task-specific inputs and outputs: ${\bf T}=\left\{T_{1:K}\right\}$, where $T_i=(X_i, Y_i)$.
The design of the task spaces can be further divided into two different settings: a single-domain setting (where all inputs are the same $X_i=X_j, i\neq j$, i.e., one-to-many mapping), and a multi-domain setting (where all inputs are different: $X_i\neq X_j, i\neq j$, i.e., many-to-many mapping). We want to optimise $\boldsymbol \theta$ for all tasks ${\bf T}$ and obtain a good performance in some pre-selected primary tasks ${\bf T}^{pri}\subseteq {\bf T}$. If ${\bf T}^{pri}= {\bf T}$, we are in the multi-task learning setting, otherwise we are in the auxiliary learning setting.
The Design of Optimisation Methods
Multi-task or auxiliary learning optimisation methods are designed to balance training and avoid negative transfer. These optimisation strategies can further be categorised into two main directions:
-
Single Objective Optimisation:
\begin{align}
\min_{ \boldsymbol \theta}\, \sum_{i=1}^K \lambda_i \cdot L_i\left(f\left(x_i; \theta_{sh}, \theta_{i}\right), y_i\right),
\end{align}
where the task-specific weightings $\boldsymbol \lambda$ are applied for a linearly combined single valued loss. Each task's influence on the network parameters can be indirectly balanced by finding a suitable set of weightings which can be manually chosen, or learned through a heuristic --- which we called weighting-based methods; or directly balanced by operating on task-specific gradients --- which we called gradient-based methods. These methods are designed exclusively to alter optimisation.
On the other hand, we also have another class of approaches that determine task groupings, which can be considered as an alternate form of weighting-based method, by finding fixed and binary task weightings indicating which tasks should be trained together. Mixing the best of both worlds, Auto-$\lambda$ is an optimisation framework, simultaneously exploring dynamic task relationships.
-
Multi-Objective Optimisation:
\begin{align}
\min_{ \boldsymbol \theta}\, \left[L_i\left(f\left(x_i; \theta_{sh}, \theta_{i}\right), y_i\right)_{i=1:K}\right]^\intercal,
\end{align}
a vector-valued loss which is optimised by achieving Pareto optimality --- when no common gradient updates can be found such that all task-specific losses can be decreased. Note that, this optimisation strategy can only be used in a multi-task learning setup.
Auto-$\boldsymbol \lambda$: Exploring Dynamic Task Relationships
Auto-$\lambda$ is a gradient-based meta learning framework, a unified optimisation strategy for both multi-task and auxiliary learning problems, which can find suitable task weightings, based on any combination of primary tasks. The design of Auto-$\lambda$ borrows the concept of looking ahead methods in meta learning literature, to update parameters at the current state of learning, based on the observed effect of those parameters on a future state. A recently proposed task grouping method TAG also applied a similar concept, computing the relationships based on how the gradient update of one task can affect the performance of other tasks. We generalise this concept by encoding task relationships explicitly with a set of task weightings associated with training loss, directly optimised based on validation loss of the primary tasks.
Let us denote ${\bf P}$ as the set of indices for all primary tasks defined in ${\bf T}^{pri}$; $(x^{val}_i, y^{val}_i)$ and $(x^{train}_i, y^{train}_i)$ are sampled from the validation and training sets of the $i^{th}$ task space, respectively. The goal of Auto-$\lambda$ is to find optimal task weightings $\boldsymbol \lambda^\ast$, which minimise the validation loss on the primary tasks, as a way to measure generalisation, where the optimal multi-task network parameters $\boldsymbol \theta^\ast$ are obtained by minimising the $\boldsymbol \lambda^\ast$ weighted training loss on all tasks. This implies the following bi-level optimisation problem:
\begin{align}
&\min_{\boldsymbol \lambda}\quad \sum_{i\in {\bf P}}L_i(f(x^{val}_i;\theta_{sh}^\ast,\theta_i^\ast), y_i^{val}) \\
&\text{s.t.}\quad \boldsymbol \theta^\ast=\text{argmin}_{\boldsymbol \theta} \sum_{i=1}^K \lambda_i \cdot L_i(f(x^{train}_i;\theta_{sh},\theta_i), y_i^{train}).
\end{align}
The above bi-level optimisation requires computing second-order gradients which may produce large memory and slow down training speed. Therefore, we additionally applied finite difference approximation and stochastic task sampling during optimisation, which allow Auto-$\lambda$ to be optimised efficiently in an end-to-end manner, with a constant memory independent of the number of training tasks.
Are Multi-task Optimisation Methods Really Useful?
There appears some recent works questioned the effectiveness of multi-task optimisation methods, showing that simply using strong regularisation strategies or randomly generated task weightings can achieve multi-task performance competitive with complex multi-task methods. This observation no doubt gives us a serious call to introspect our recent development in multi-task learning research.
My personal perspective is that this observation might be only true given the fact that these training tasks are strongly related to each other --- e.g., datasets like Multi-MNIST and CelebA both have very similar label distribution across tasks; or simply the current multi-task benchmarks are just too easy. Applying multi-task optimisation methods on top of these datasets is no surprised to have a marginal effect. As also proven by a recently developed generalist agent: GATO by DeepMind, training on large-scale tasks in different modalities does not necessarily/automatically leads to cross-modality generalisation. In the presence of finite model capacity, how to achieve stronger cross-modality generalisation with large-scale multi-task learning remains an open question.
On the other hand, I'd like to argue that another interesting and important application of multi-task learning is auxiliary learning, which has been unfortunately a bit overlooked from the community. In most cases, we only care about the performance of a few tasks (usually only one task), supported with a large set of proxy tasks available that may or may not be helpful for these primary tasks. Finding the most suitable proxy tasks to assist learning of these primary tasks are not trivial, and a good optimisation strategy designed for auxiliary learning will by design lead to a much stronger effect compared to multi-task learning methods. We will show in details in the following sections.
Experiments
Baselines
In multi-task experiments, we compared Auto-$\lambda$ with state-of-the-art weighting-based multi-task optimisation methods: i) Equal weighting, ii) Uncertainty weighting, and iii) Dynamic Weight Average. In auxiliary learning experiments, we only compared with Gradient Cosine Similarity (GCS) due to the limited works for this setting.
Results on Dense Prediction Tasks
Here, we evaluated Auto-$\lambda$ with dense prediction tasks in NYUv2 and CityScapes, two standard multi-task datasets in a single-domain setting. In NYUv2, we trained on 3 tasks: 13-class semantic segmentation, depth prediction, and surface normal prediction, with the same experimental setting as in our previous project MTAN. In CityScapes, we trained on 3 tasks: 19-class semantic segmentation, disparity (inverse depth) estimation, and a recently proposed 10-class part segmentation, with the same experimental setting as in Uncertainty. In both datasets, we trained on two multi-task architectures: Split: the standard multi-task learning architecture with hard parameter sharing, which splits at the last layer for the final prediction for each specific task; MTAN: a state-of-the-art multi-task architecture based on task specific feature-level attention. Both networks were based on ResNet-50 as the backbone architecture.
Noise Prediction as Sanity Check:
In auxiliary learning, we additionally trained with a noise prediction task along with the standard three tasks defined in a dataset. The noise prediction task was generated by assigning a random noise map sampled from a Uniform distribution for each training image. This task is designed to test the effectiveness of different auxiliary learning methods in the presence of useless gradients. We trained from scratch for a fair comparison among all methods in our experiments.
We show quantitative results for NYUv2 and CityScapes trained with Split architecture in the following table. Please check our technical paper for results in other datasets and with other multi-task architectures.
| NYUv2 |
Method |
Sem. Seg. [mIoU $\uparrow$] |
Depth [aErr. $\downarrow$] |
Normal [mDist. $\downarrow$] |
$\Delta$ MTL $\uparrow$ |
| Single Task |
- |
43.37 |
52.24 |
22.40 |
- |
| Multi-task |
Equal |
44.64 |
43.32 |
24.48 |
+3.57% |
| DWA |
45.14 |
43.06 |
24.17 |
+4.58% |
| Uncertainty |
45.98 |
41.26 |
24.09 |
+6.50% |
| Auto-$\lambda$ |
47.17 |
40.97 |
23.68 |
+8.21% |
| Auxiliary Task |
Uncertainty |
45.26 |
42.25 |
24.36 |
+4.91% |
| GCS |
45.01 |
42.06 |
24.12 |
+5.20% |
| Auto-$\lambda$ [3 Tasks] |
48.04 |
40.61 |
23.31 |
+9.66% |
| Auto-$\lambda$ [1 Task] |
47.80 |
40.27 |
23.09 |
+10.02% |
| CityScapes |
Method |
Sem. Seg. [mIoU $\uparrow$] |
Part Seg. [mIoU $\uparrow$] |
Disp. [aErr. $\downarrow$] |
$\Delta$ MTL $\uparrow$ |
| Single Task |
- |
56.20 |
52.74 |
0.84 |
- |
| Multi-task |
Equal |
54.03 |
50.18 |
0.79 |
-0.92% |
| DWA |
54.93 |
50.15 |
0.80 |
-0.80% |
| Uncertainty |
56.06 |
52.98 |
0.82 |
+0.86% |
| Auto-$\lambda$ |
56.08 |
51.88 |
0.76 |
+2.56% |
| Auxiliary Task |
Uncertainty |
55.72 |
52.62 |
0.83 |
+0.04% |
| GCS |
55.76 |
52.19 |
0.80 |
+0.98% |
| Auto-$\lambda$ [3 Tasks] |
56.42 |
52.42 |
0.78 |
+2.31% |
| Auto-$\lambda$ [1 Task] |
57.89 |
53.56 |
0.77 |
+4.30% |
Performance on NYUv2 and CityScapes datasets with multi-task and auxiliary learning methods in Split multi-task architecture. Auxiliary learning is additionally trained with a noise prediction task. Results are averaged over two independent runs, and the best results are highlighted in bold.
Our Auto-$\lambda$ outperformed all baselines in multi-task and auxiliary learning settings across both multi-task networks, and has a particularly prominent effect in auxiliary learning setting where it doubles the relative overall multi-task performance compared to auxiliary learning baselines.
We show results for two auxiliary task settings: optimising for just one task (Auto-$\lambda$ [1 Task]), where the other three tasks (including noise prediction) are purely auxiliary, and optimising for all three tasks (Auto-$\lambda$ [3 Tasks]), where only the noise prediction task is purely auxiliary. Auto-$\lambda$ [3 Tasks] has nearly identical performance to Auto-$\lambda$ in a multi-task learning setting, whereas the best multi-task baseline Uncertainty achieved notably worse performance when trained with noise prediction as an auxiliary task. This shows that standard multi-task optimisation is susceptible to negative transfer, whereas Auto-$\lambda$ can avoid negative transfer due to its ability to minimise $\bf \lambda$ for tasks that do not assist with the primary task. We also show that Auto-$\lambda$ [1 Task] can further improve performance relative to Auto-$\lambda$ [3 Tasks], at the cost of task-specific training for each individual task.
Intriguing Learning Strategies in Auto-$\boldsymbol \lambda$
In this section, we visualise and analyse the learned weightings from Auto-$\lambda$, and find that Auto-$\lambda$ is able to produce interesting learning strategies with interpretable relationships. Specifically, we focus on using Auto-$\lambda$ to understand the underlying structure of tasks and transferred task knowledge, introduced next.
Understanding The Structure of Tasks
Observation #1: Task relationships are consistent.
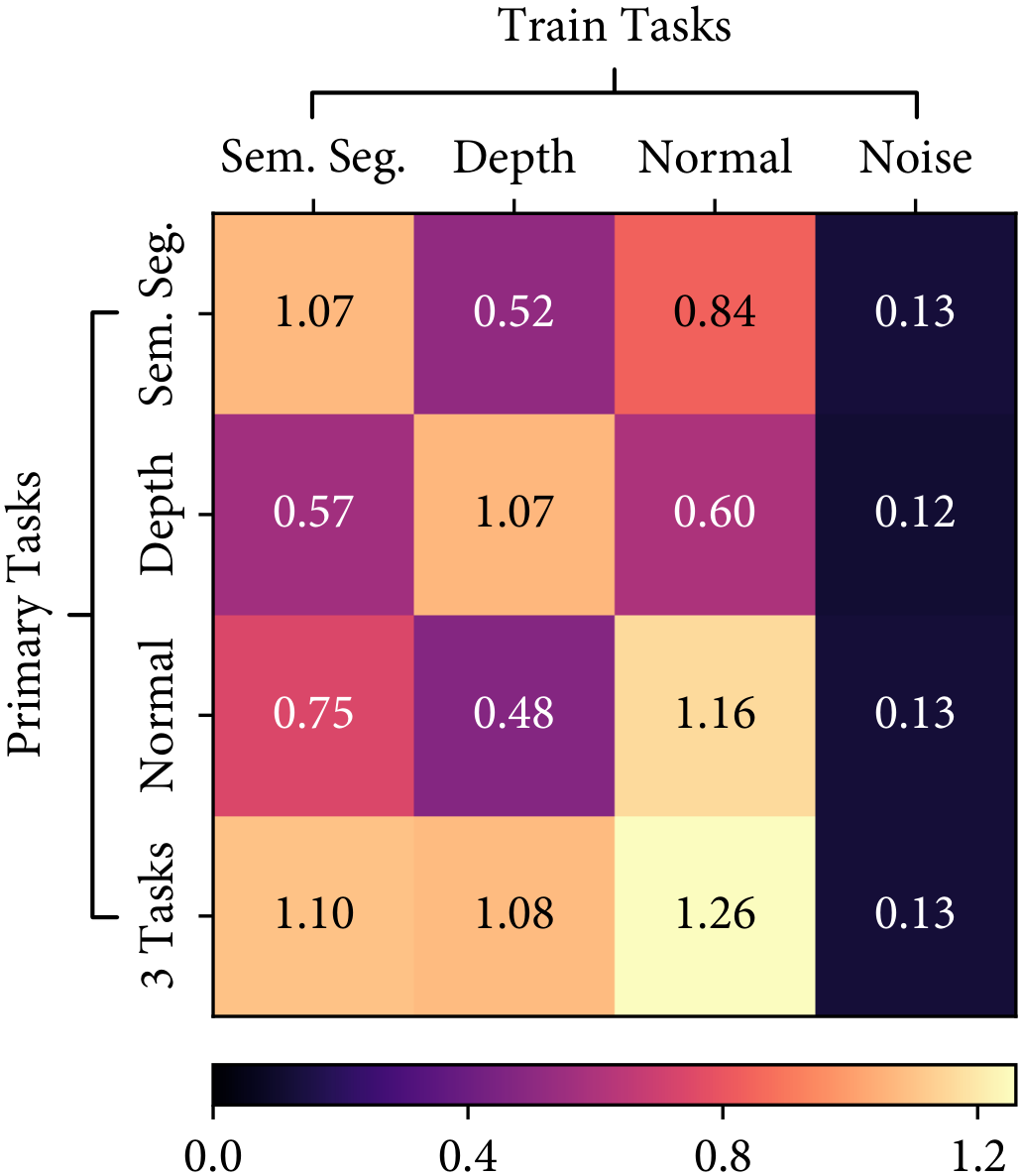
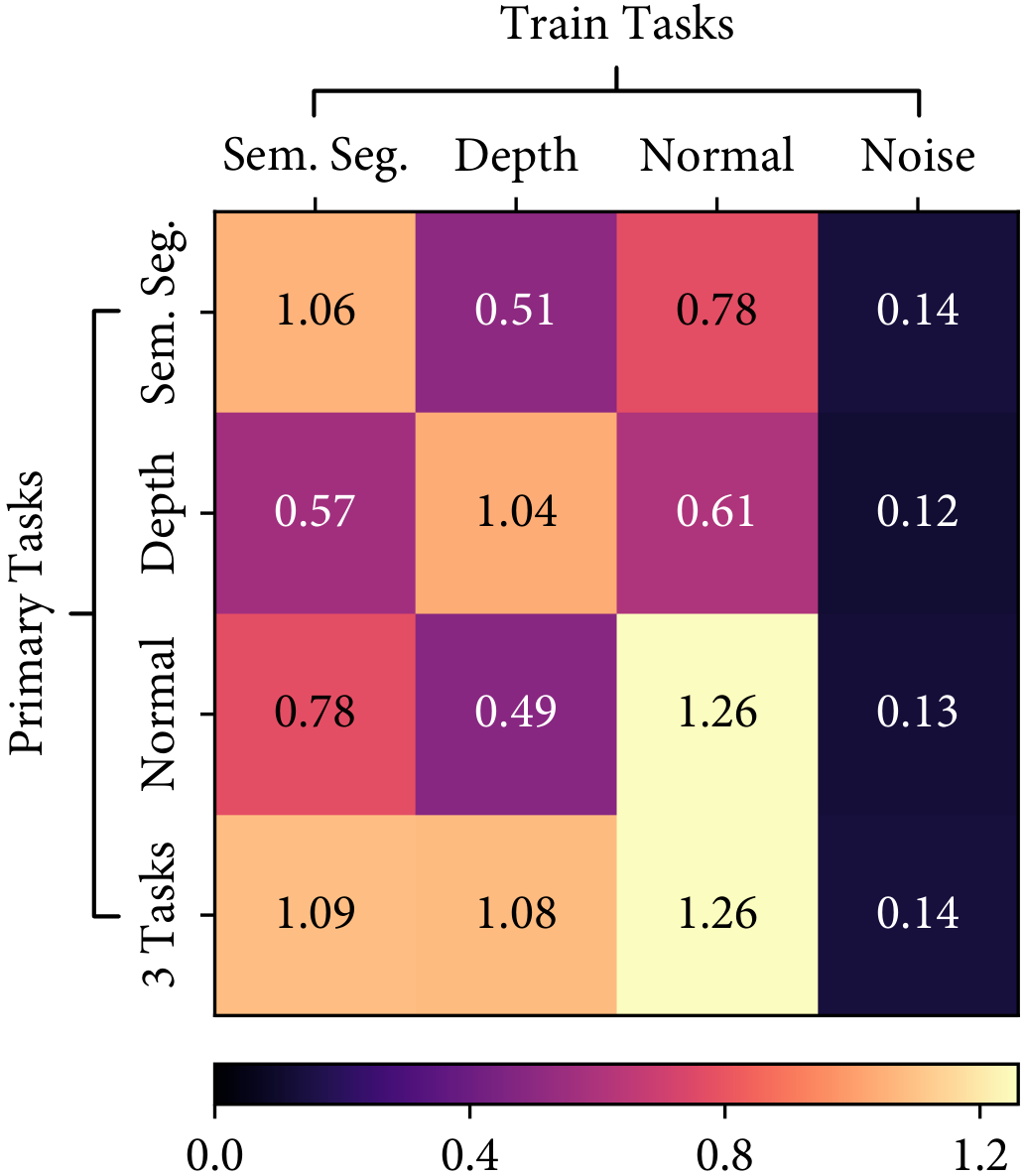
Firstly, we observe that the structure of tasks is consistent across the choices of learning algorithms. As shown in the following figure, the learned weightings of both NYUv2 and CityScapes datasets are nearly identical, given the same optimisation strategies, independent of the network architectures.
NYUv2 - Split
NYUv2 - MTAN
CityScapes - Split
CityScapes - MTAN
Auto-$\lambda$ explored consistent task relationships in NYUv2 and CityScapes datasets for both Split and MTAN architectures. Higher task weightings indicate stronger relationships, and lower task weightings indicate weaker relationships.
Observation #2: Task relationships are asymmetric.
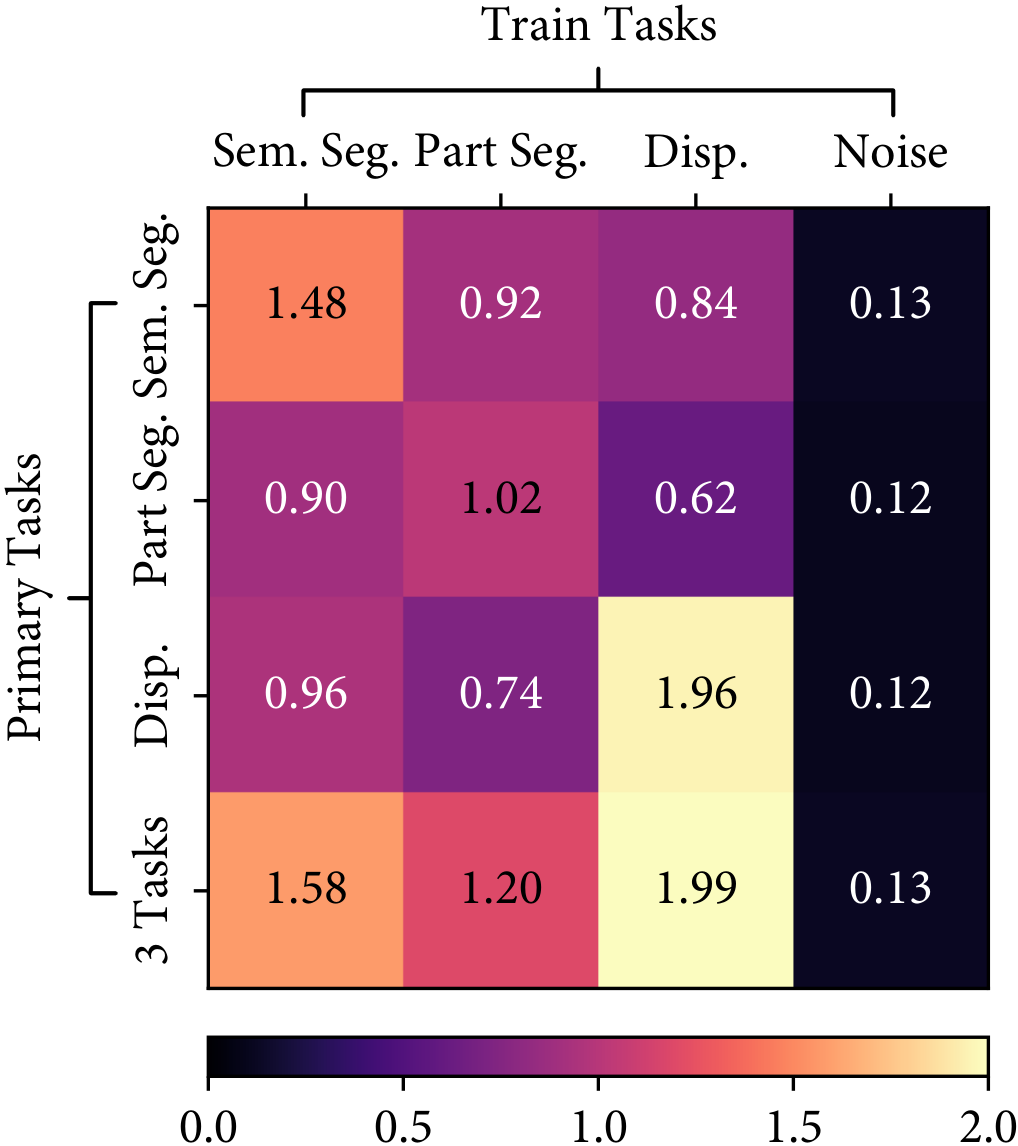
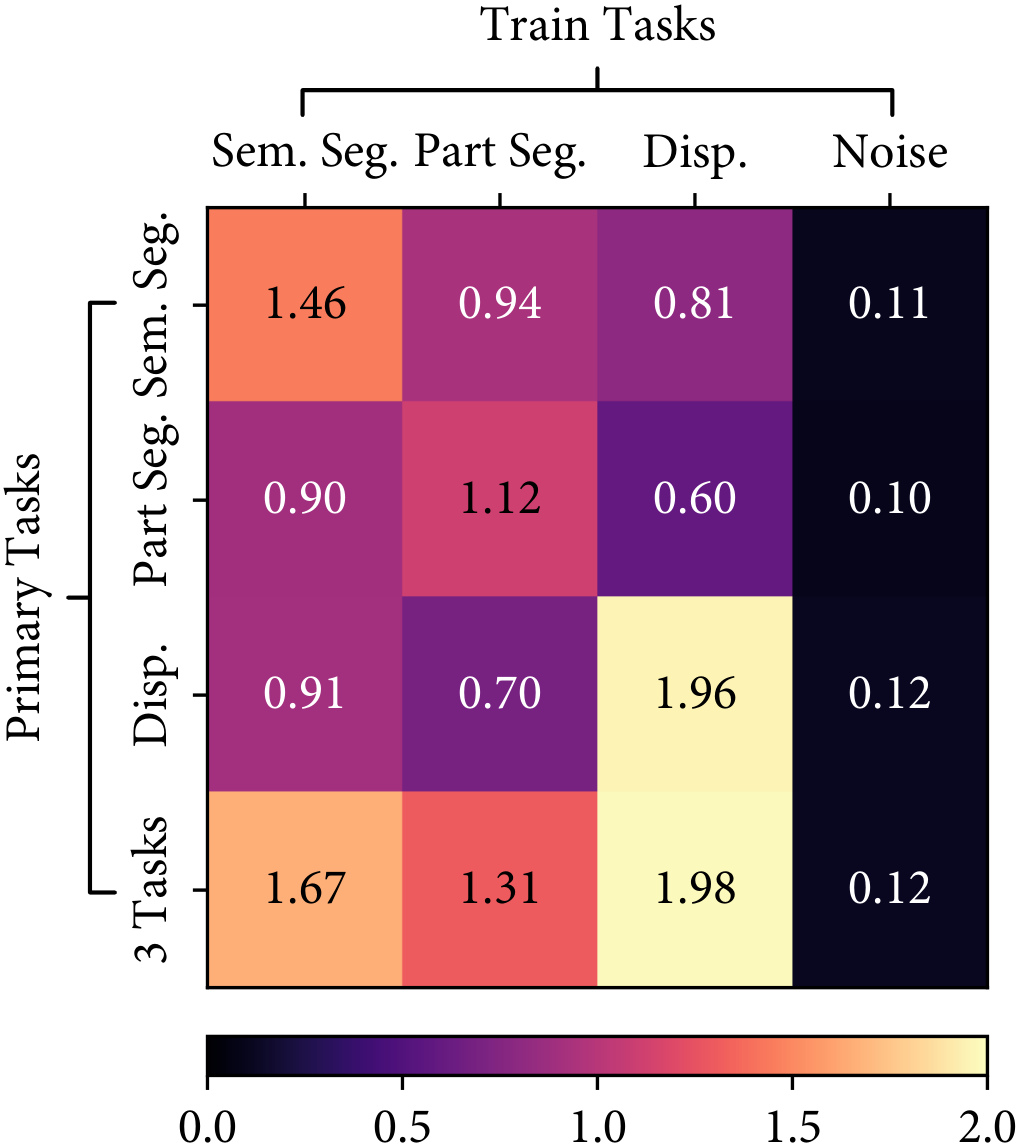
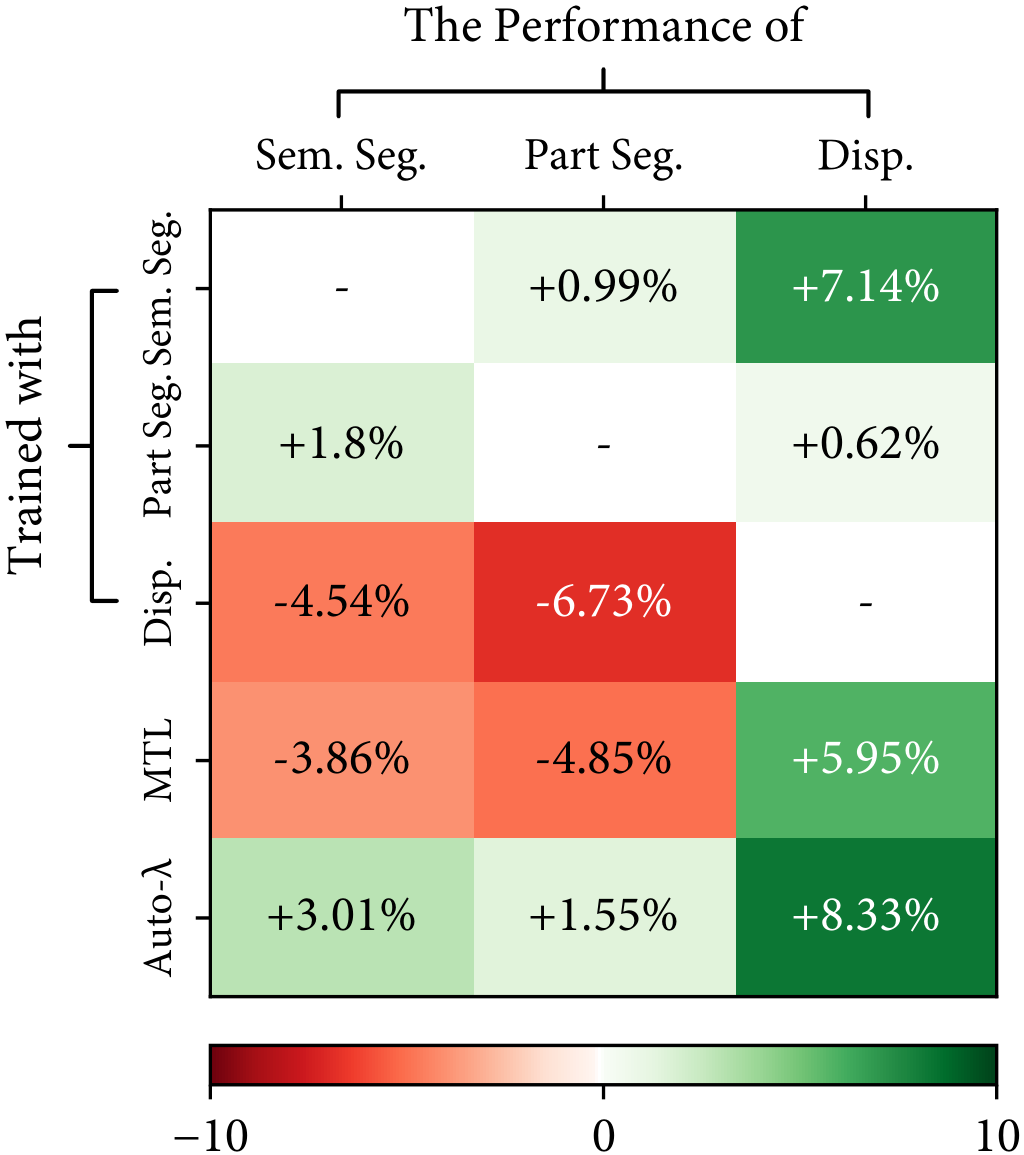
We also found that the task relationships are asymmetric, i.e. learning task $A$ with the knowledge of task $B$ is not equivalent to learning task $B$ with the knowledge of task $A$. A simple example is shown in the following figure, where the semantic segmentation task in CityScapes helps the part segmentation task much more than the part segmentation helps the semantic segmentation. This also follows intuition: the representation required for semantic segmentation is a subset of the representation required for part segmentation.
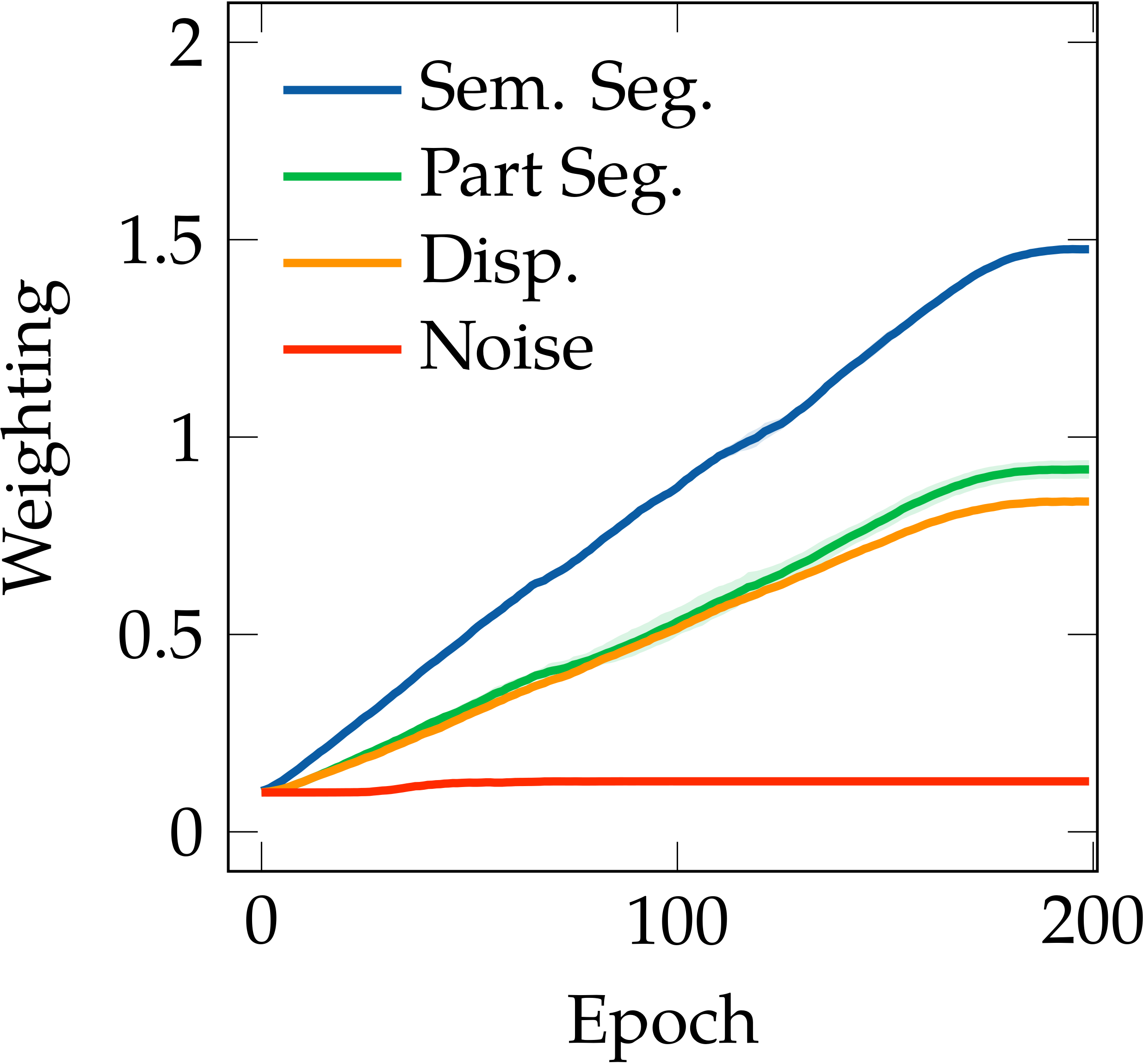
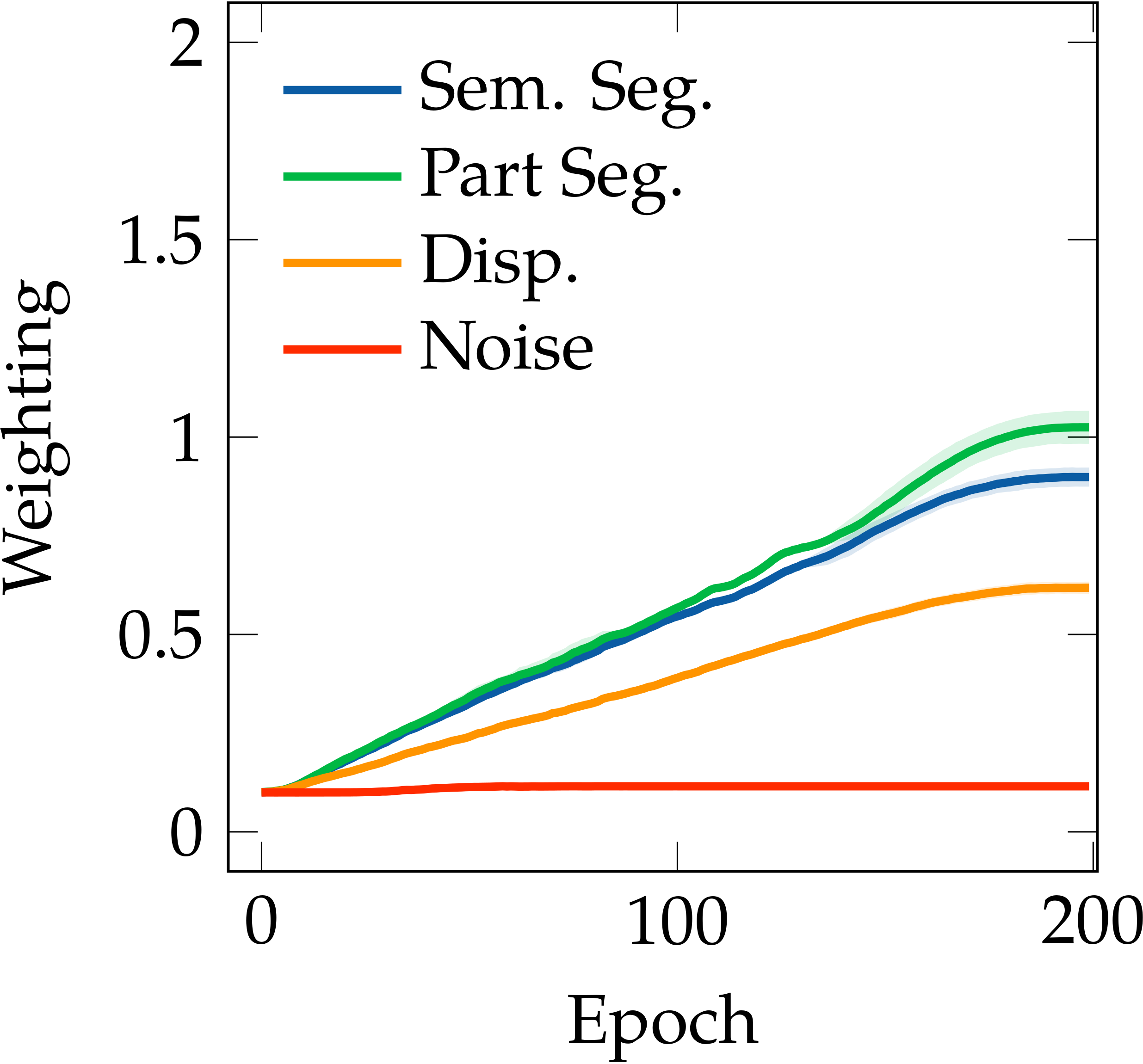
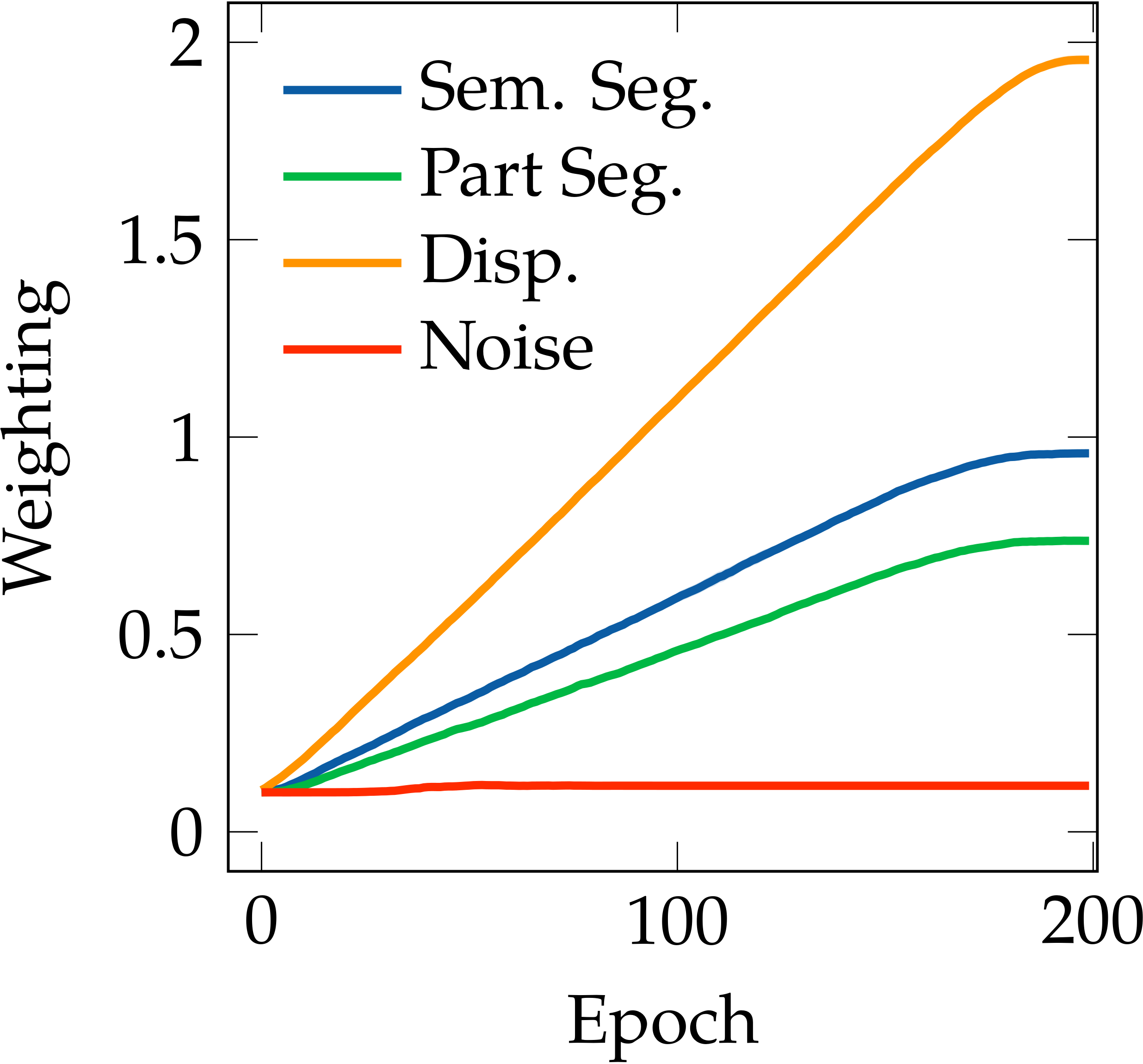
CityScapes - [Sem. Seg.]
CityScapes - [Part Seg.]
CityScapes - [Disp.]
Auto-$\lambda$ learned dynamic relationships based on the choice of primary tasks. $[\cdot]$ represents the choice of primary tasks.
Observation #3: Task relationships are dynamic.
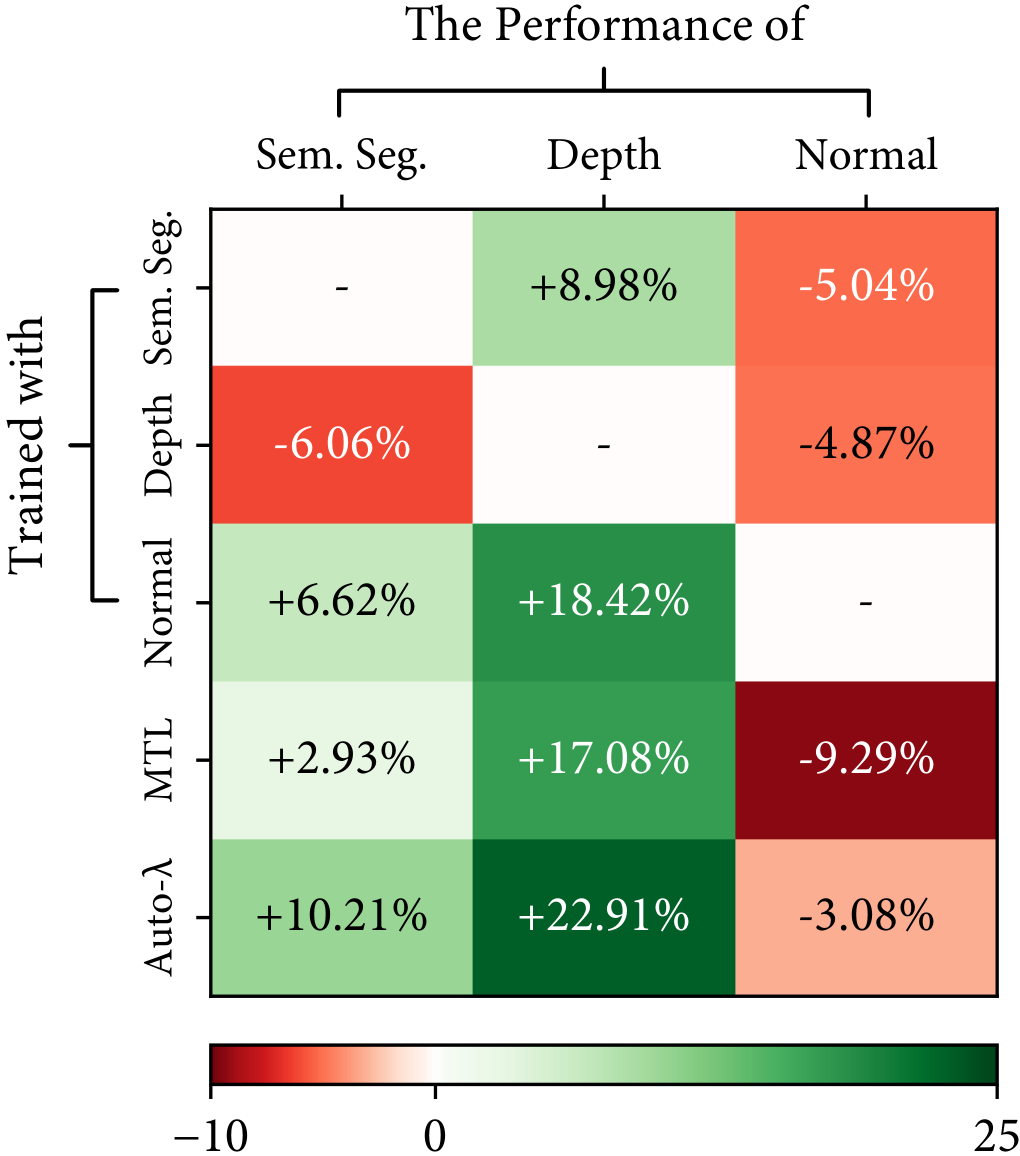
A unique property of Auto-$\lambda$ is the ability to explore dynamic task relationships. As shown in the following figure Left, we can observe a weighting cross-over appears in NYUv2 near the end of training, which can be considered as a learning strategy of automated curricula. Further, in the figure Right, we verify that Auto-$\lambda$ achieved higher per-task performance compared to every combination of fixed task groupings in NYUv2 and CityScapes datasets. We can also observe that the task relationships inferred by the fixed task groupings is perfectly aligned with the relationships learned with Auto-$\lambda$. In addition, we can observe that the Uncertainty method is not able to avoid negative transfer from the noise prediction task, having a constant weighting across the entire training stage, which leads to a degraded multi-task performance as observed in Experiment section. These observations confirm that Auto-$\lambda$ is an advanced optimisation strategy, and is able to learn accurate and consistent task relationships.
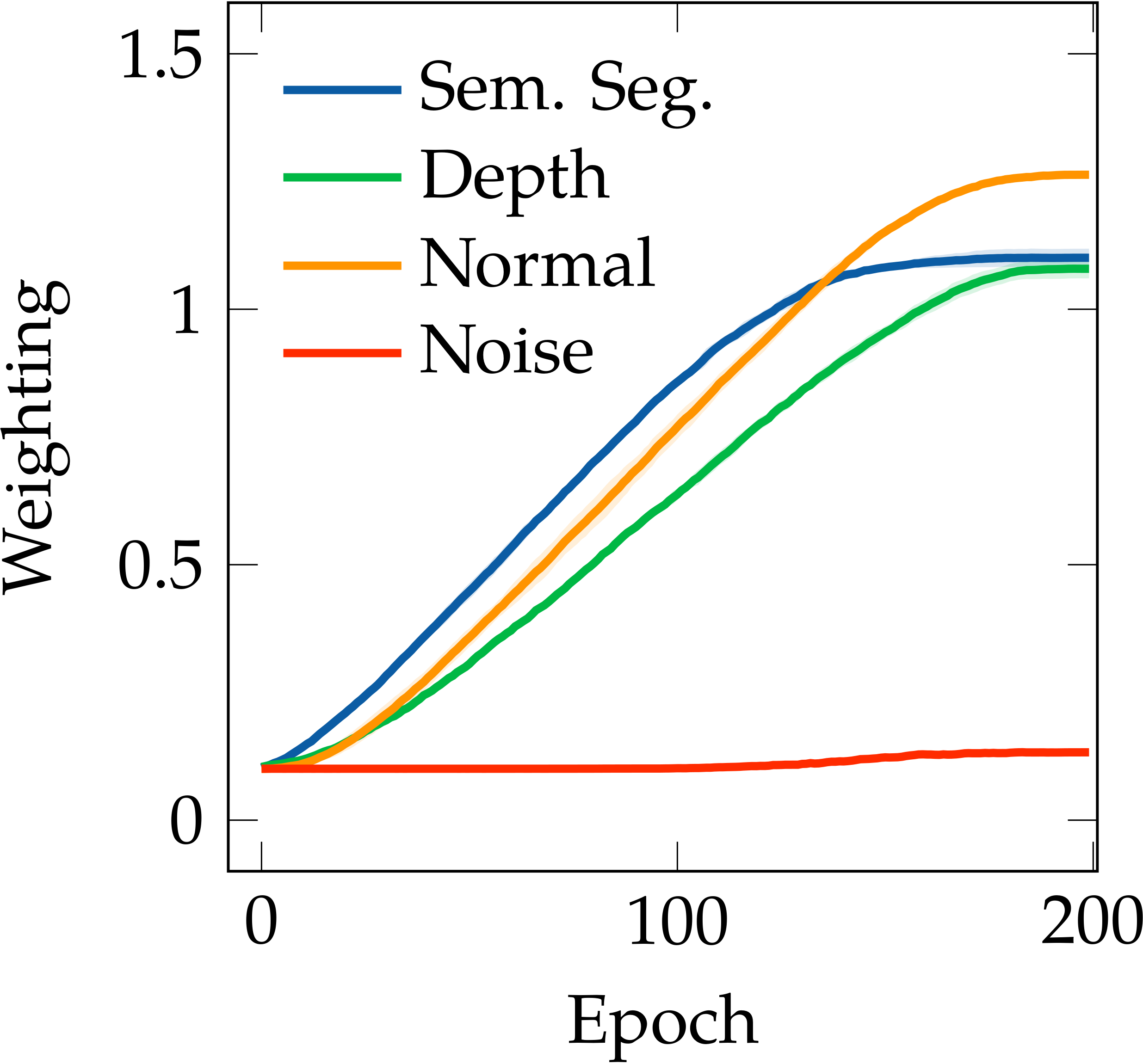
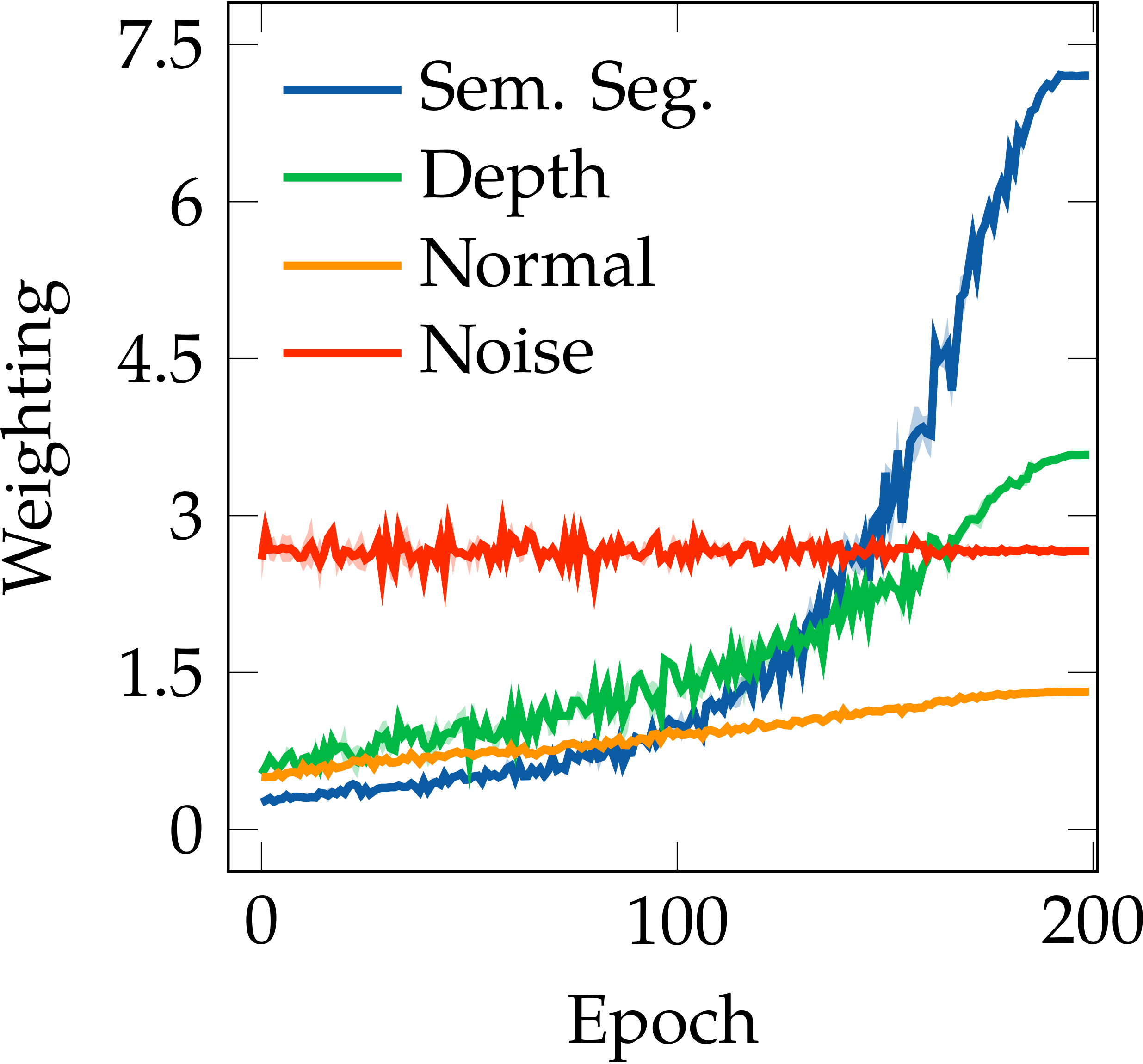
NYUv2 - [3 Tasks]
NYUv2 - Uncertainty
NYUv2
CityScapes
Left: Auto-$\lambda$ can avoid negative transfer based on the choice of primary tasks, whilst Uncertainty method is not able to avoid negative transfer, having a constant weighting on noise prediction task across the entire training stage. Right: Auto-$\lambda$ achieved best per-task performance compared to every combination of fixed task groupings in NYUv2 and CityScapes trained with Split architecture.
Understanding The Transferred Task Knowledge (Blue Sky Thinking)
Apart from understanding task relationships, we found that Auto-$\lambda$ can also help us discover interesting transferred task knowledge, which would be useful for choosing/designing suitable auxiliary tasks.
Please note that: some of the observations might be only true in specific datasets and training strategies. We consider this section a blue sky thinking with open-ended discussion which aims to explore interesting insights.
Skills v.s. Geometry
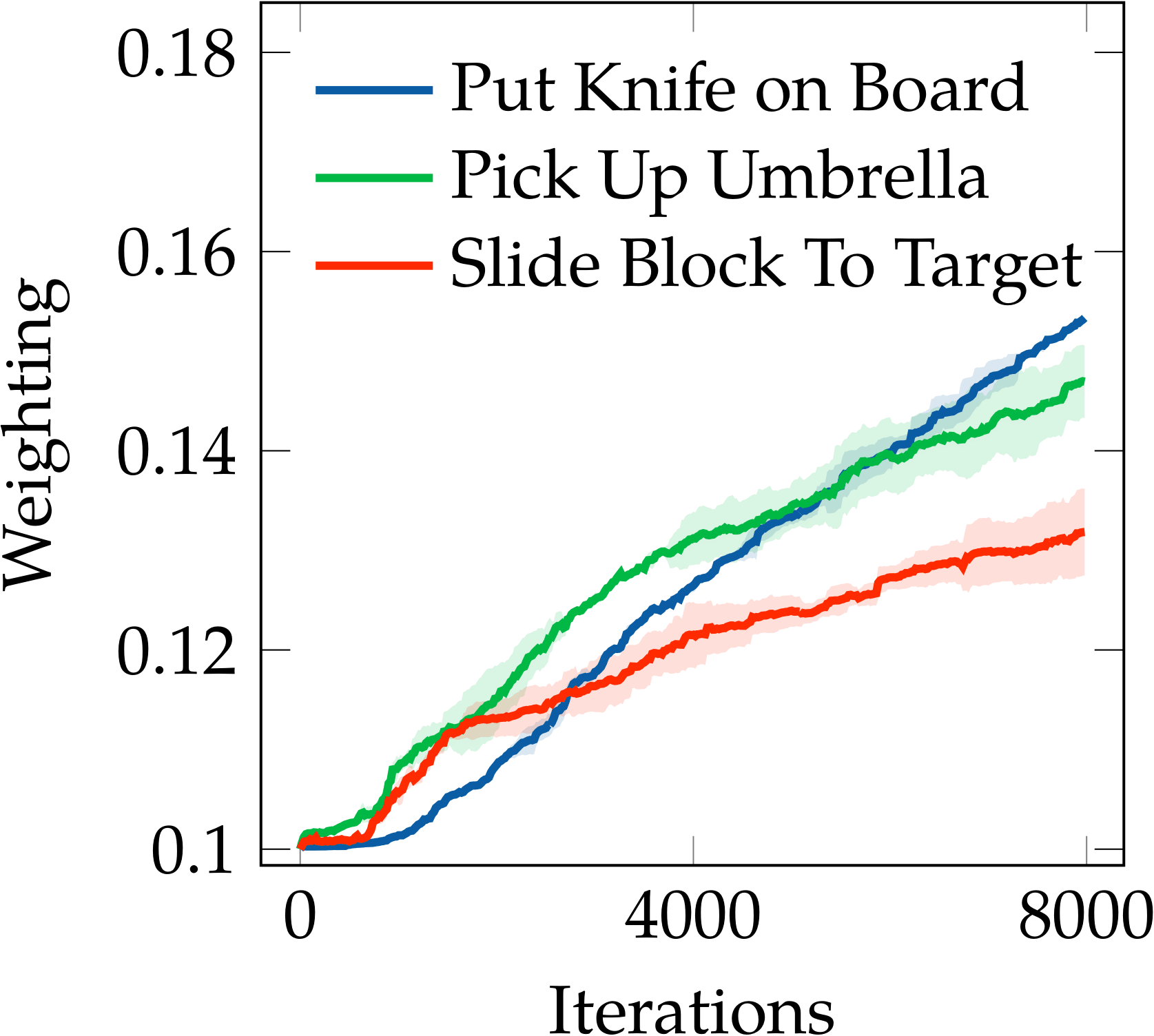
For the robot manipulation tasks, we found out that Auto-$\lambda$ has a clear prioritisation on optimising weightings based on skills (or task trajectories) rather than object geometry or appearance. For example, as shown in the following figure, “pick up umbrella” and “pick up cup” are the two most related tasks for “pick and lift”; all of these tasks require a grasp and lift skill, but the geometry differs across the tasks. Similarly, “pick up umbrella” and “slide block to target” are the two most related tasks for “put knife on board”; all of these tasks require the skill to displace an object from one place to another on the table, but again, the geometry differs across each task.
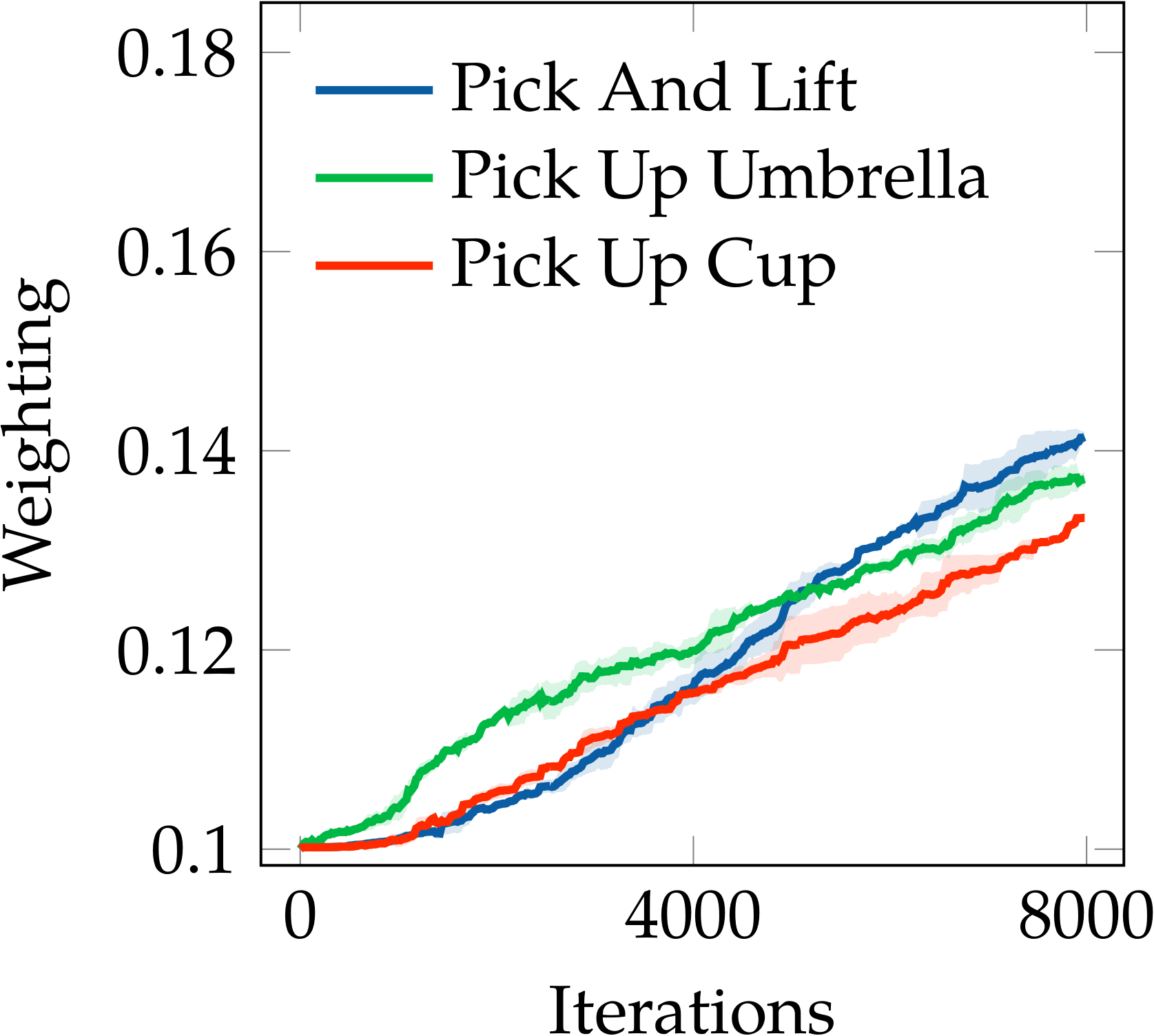
RLBench - [Pick and Lift]
RLBench - [Put Knife on Board]
Auto-$\lambda$ prioritised on skills in robotic manipulation tasks.
In-Domain v.s. Out-Domain
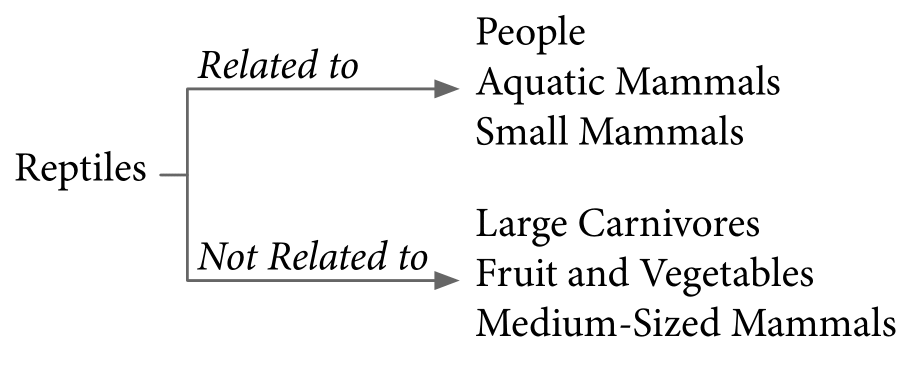
In multi-domain classification tasks, we observed that the related domains to the primary task found by Auto-$\lambda$ are not always semantically connected. For example, Fish and Small Mammals are semantically related to Aquatic Mammals because they are all small-size animals; Aquatic Mammals and Fish might share similar features related to water-like environment. However, Trees are not semantically related based on human intuition. Similarly, we will consider Aquatic Mammals and Small Mammals to be related to Reptiles, but not for People. This shows that domain-specific knowledge may require out-of-domain knowledge to improve generalisation. A similar observation is also found in our previous project MAXL, showing the optimal auxiliary tasks are not easily interpretable. This interesting observation occurs in many domains in CIFAR-100 dataset, and the full relationship structure is included in the technical paper.
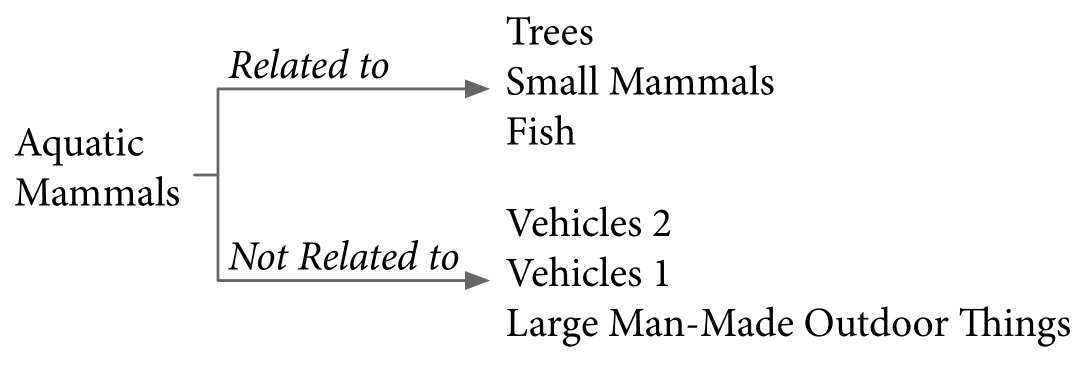
CIFAR-100 - [Aquatic Mammals]
CIFAR-100 - [Reptiles]
Top 3 related and unrelated domains with Aquatic Mammals and Reptiles in multi-domain CIFAR-100 classification task.
Conclusions, Limitations and Discussion
In this paper, we have presented Auto-$\lambda$, a unified multi-task and auxiliary learning optimisation framework. Auto-$\lambda$ operates by exploring task relationships in the form of task weightings in the loss function, which are allowed to dynamically change throughout the training period. This allows optimal weightings to be determined at any one point during training, and hence, a more optimal period of learning can emerge than if these weightings were fixed throughout training. Auto-$\lambda$ achieves state-of-the-art performance in both computer vision and robotics benchmarks, for both multi-task learning and auxiliary learning, even when compared to optimisation methods that are specifically designed for just one of those two settings.
For transparency, we now discuss some limitations of Auto-$\lambda$ that we have noted during our implementations, and we discuss our thoughts on future directions with this work.
Hyper-parameter Search:
To achieve optimal performance, Auto-$\lambda$ still requires hyper-parameter search (although the performance is primarily sensitive to only one parameter, the learning rate, making this search relatively simple). Some advanced training techniques, such as incorporating weighting decay or bounded task weightings, might be helpful to find a general set of hyper-parameters which work for all datasets.
Training Speed:
The design of Auto-$\lambda$ requires computing second-order gradients, which is computationally expensive. To address this, we applied a finite-difference approximation scheme to reduce the complexity, which requires the addition of only two forward passes and two backward passes. However, this may still be slower than alternative optimisation methods.
Single Task Decomposition:
Auto-$\lambda$ can optimise on any type of task. Therefore, it is natural to consider a compositional design, where we decompose a single task into multiple small sub-tasks, e.g. to decompose a multi-stage manipulation tasks into a sequence of stages. Applying Auto-$\lambda$ on these sub-tasks might enable us to explore interesting learning behaviours to improve single task learning efficiency.
Open-ended Learning:
Given the dynamic structure of the tasks explored by Auto-$\lambda$, it would be interesting to study whether Auto-$\lambda$ could be incorporated into an open-ended learning system, where tasks are continually added during training. The flexibility of Auto-$\lambda$ to dynamically optimise task relationships may naturally facilitate open-ended learning in this way, without requiring manual selection of hyper-parameters for each new task.
Citation
If you found this work is useful in your own research, please considering citing the following.
@article{liu2022auto_lambda,
title={Auto-Lambda: Disentangling Dynamic Task Relationships},
author={Liu, Shikun and James, Stephen and Davison, Andrew J and Johns, Edward},
journal={Transactions on Machine Learning Research},
year={2022}
}

















