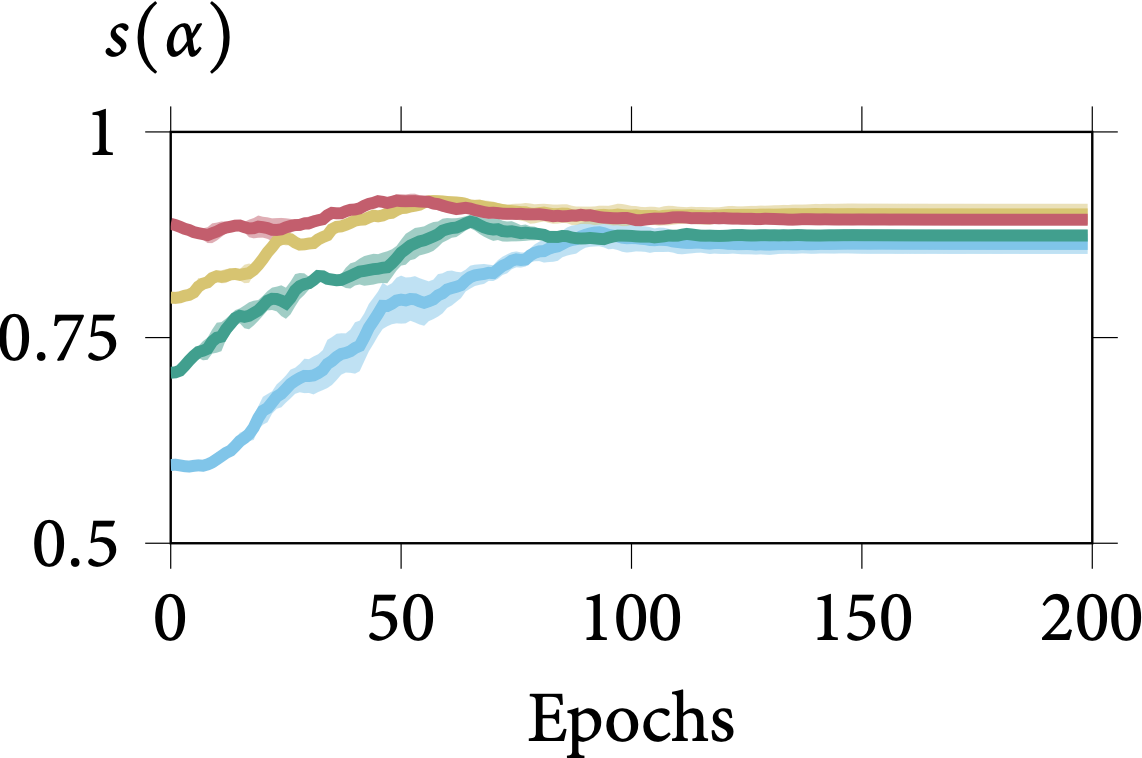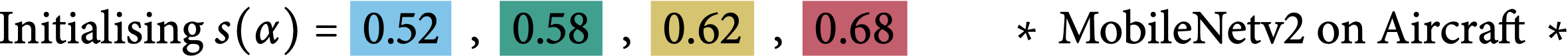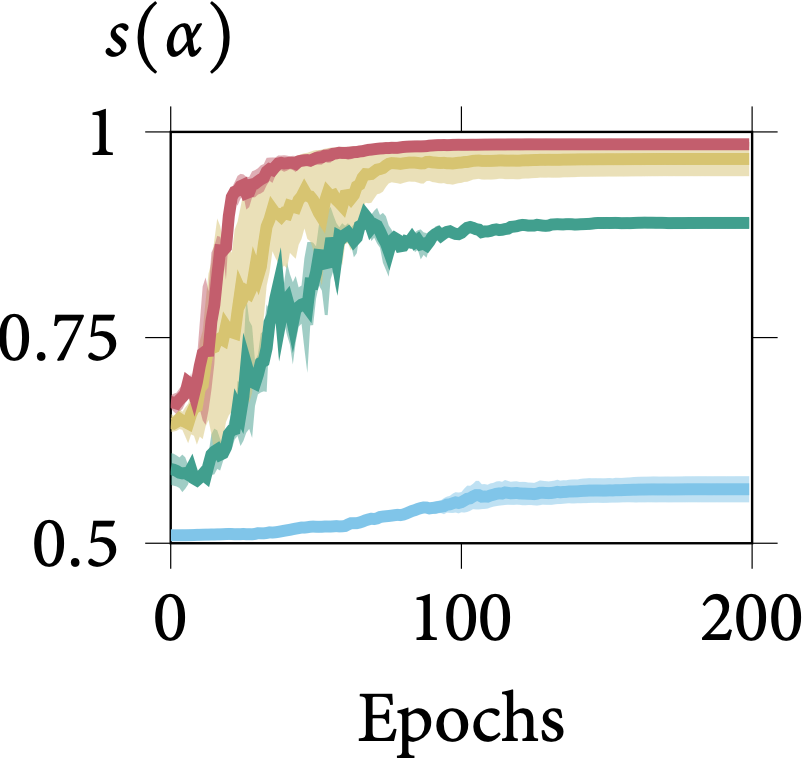Shape Adaptor
by Shikun Liu, Zhe Lin, Yilin Wang, Jianming Zhang, Federico Perazzi, & Edward Johns
We present a novel resizing module for convolutional neural networks: shape adaptor, a drop-in enhancement built on top of traditional resizing layers, such as pooling, bilinear sampling, and strided convolution. Whilst traditional resizing layers have fixed and deterministic reshaping factors, our module allows for a learnable reshaping factor. Results show that by simply using a set of our shape adaptors instead of the original resizing layers, performance increases consistently over human-designed networks.
Introduction
A typical human-designed convolutional neural architecture is composed of two types of
computational modules:
-
Normal layer, such as a stride-1 convolution or an identity mapping, which maintains the spatial dimension of incoming feature maps.
-
Resizing layer,
such as max/average pooling, bilinear sampling, or stride-2 convolution, which reshapes the incoming feature map into a different spatial dimension.
We hereby define the shape of a neural network as the composition of the feature dimensions in all network layers, and the architecture as the overall structure formed by stacking multiple normal and resizing layers.
To move beyond the limitations of human-designed network architectures, there has been a
growing interest in developing Automated Machine Learning (AutoML) algorithms automatic architecture design, known as Neural Architecture Search (NAS).
However, whilst this has shown promising results in discovering powerful network architectures, these methods still rely heavily on human-designed network shapes, and focus primarily on learning connectivities between layers. Typically, reshaping factors of 0.5 (downsampling) and 2 (up-sampling) are chosen, and the total number of reshaping layers is defined manually, but we argue that network shape is an important inductive bias which should be directly optimised.
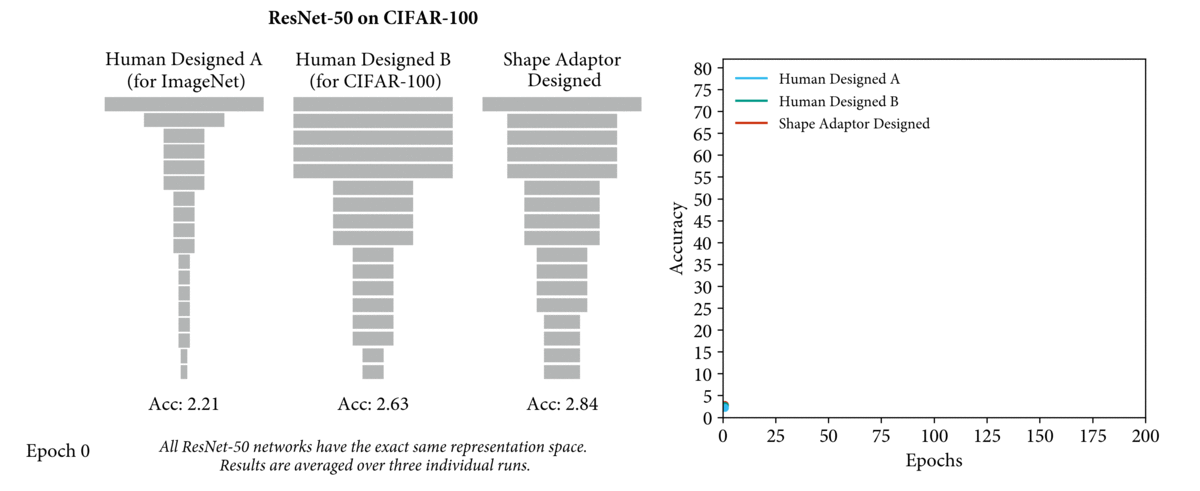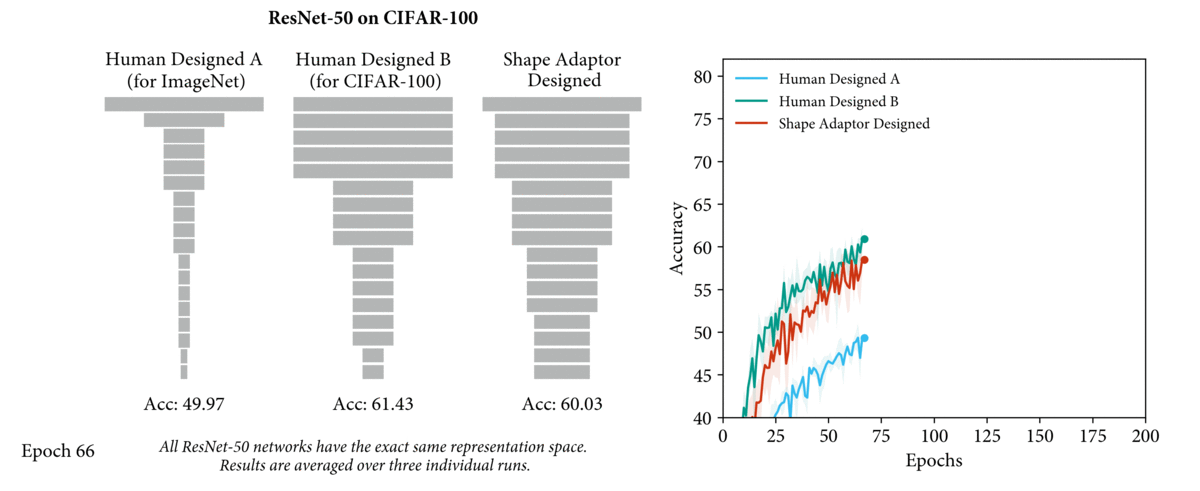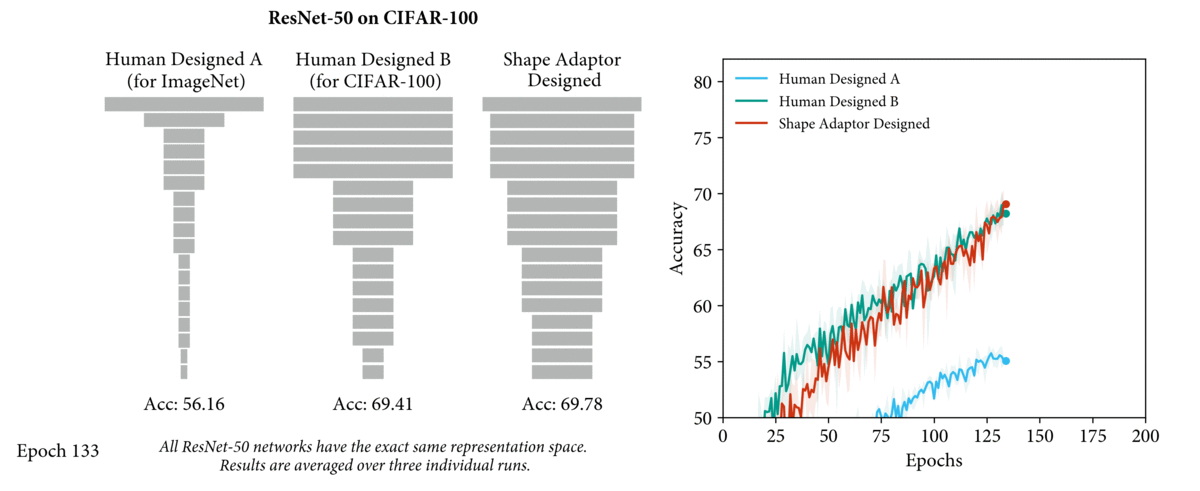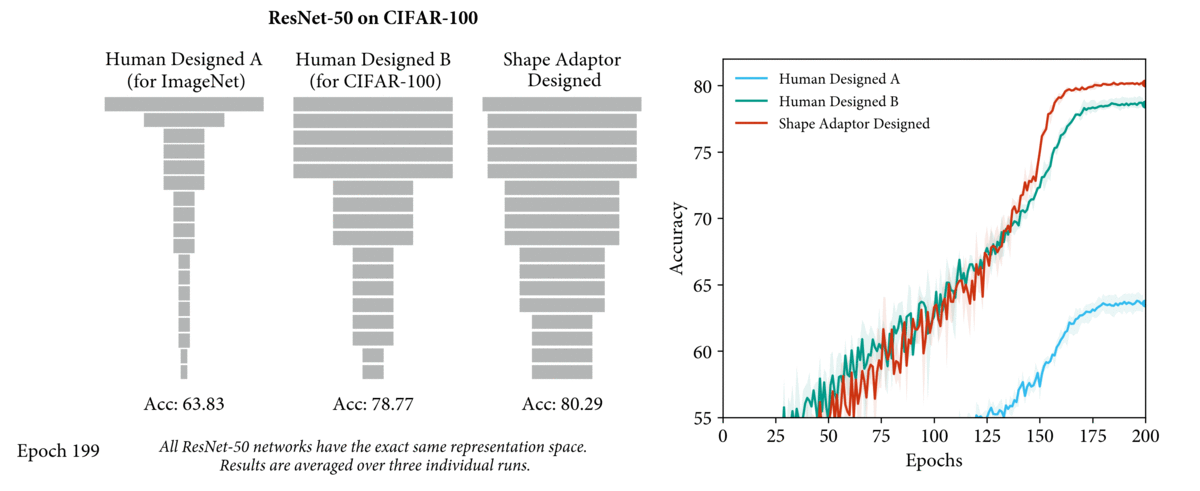
For example, the video above shows three networks with the exact same design of network
structure, but different shapes (shown in grey rectangle). For the two human-designed networks, we see that a ResNet-50 model designed specifically for CIFAR-100 dataset (Human Designed B) leads to
a 15% performance increase over a ResNet-50 model designed for ImageNet dataset (Human
Designed A). The performance can be further improved with the network shape designed
by the shape adaptors we will later introduce. Therefore, by learning network shapes rather
than manually designing them, a more optimal network architecture can be found.
The Design of Shape Adaptor
Shape Adaptor is a two-branch architecture composed of two different resizing layers $F_{1,2}$, taking the same feature map as the input. A resizing layer can be any classical sampling layer, such as max pooling, average pooling, bilinear sampling, or strided convolution, with a fixed reshaping factor $r_{1,2}$. Each resizing layer reshapes the input feature map by this factor, which represents the ratio of spatial dimension between the output and input feature maps, and outputs an intermediate feature. An adaptive resizing layer with a learnable reshaping factor is then used to reshape these intermediate features into the same spatial dimension, and combine them with a weighted average to compute the module's output.
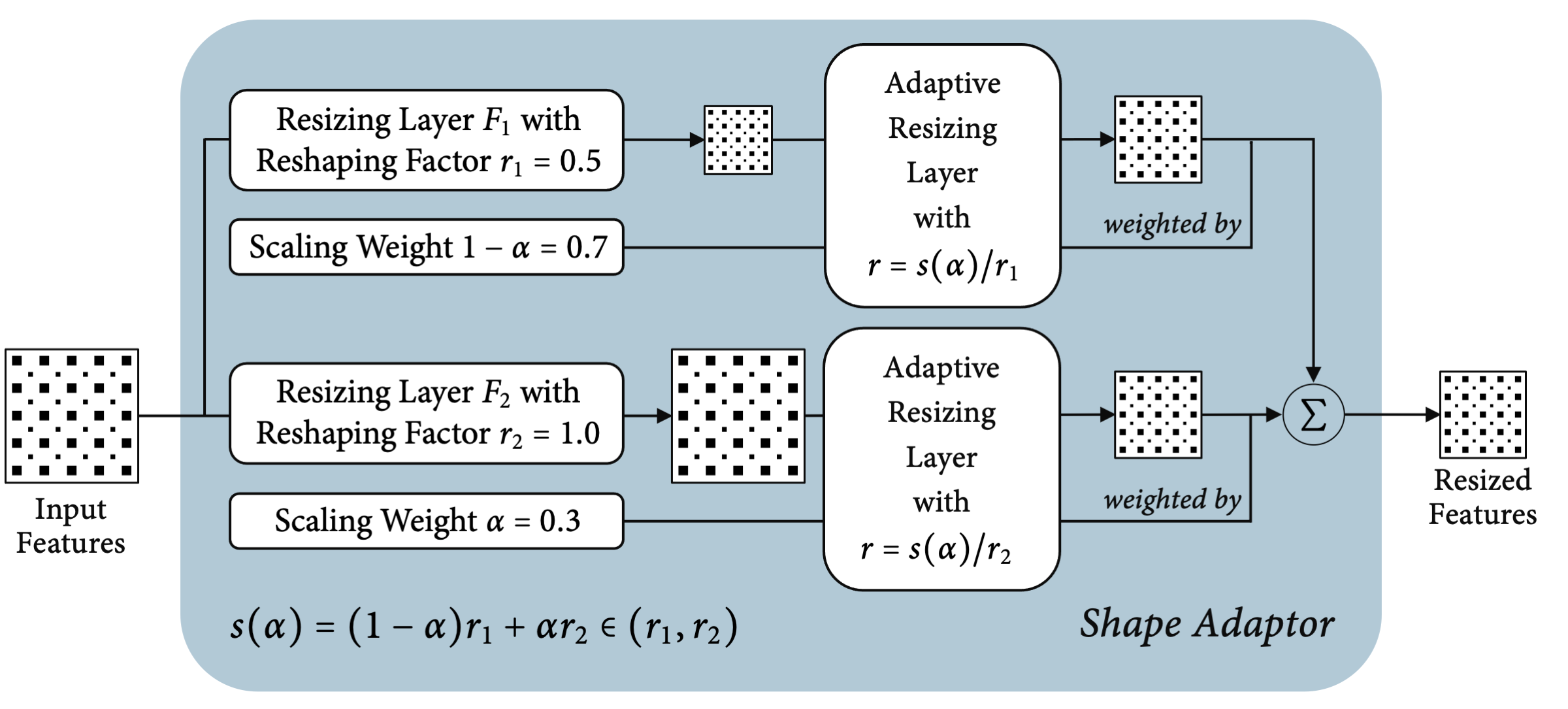
A visual illustration of a shape adaptor module.
Each module has a learnable parameter $\alpha \in (0, 1)$, parameterised by a sigmoid function, which is the only extra learnable parameter introduced by shape adaptors. The role of $\alpha$ is to optimally combine two intermediate features after reshaping them by an adaptive resizing layer. To enable a non-differential reshaping factor to be learned, we use a monotone
function $s$, which monotonically maps from $\alpha$ into the search space $s(\alpha) \in (r_1, r_2)$,
representing the scaling ratio of the module’s reshaping operation. With this formulation, a
learnable reshaping factor $s(\alpha)$ allows a shape adaptor to reshape at any scale between $r_1$ and
$r_2$, rather than being restricted to a discrete set of scales as with typical manually-designed
network architectures.
Shape adaptor is easy to implement, with only a couple of lines of PyTorch code presented below.
def shape_adaptor(input1, input2, r1, r2, alpha):
"""
input1: input feature map F1 with resizing factor r1
input2: input feature map F2 with resizing factor r2
alpha: learnable parameter (before sigmoid)
"""
# compute sigmoid of alpha
sigmoid_alpha = torch.sigmoid(alpha)
# the reshaping factor of shape adaptor
s_alpha = (r2 - r1) * sigmoid_alpha.item() + r1
# reshaping F1 and F2 with the learned reshaping factor s_alpha
input1_rs = F.interpolate(input1, scale_factor=s_alpha/r1, mode='bilinear', align_corners=True)
input2_rs = F.interpolate(input2, size=input1_rs.shape[-2:], mode='bilinear', align_corners=True)
return (1 - sigmoid_alpha) * input1_rs + sigmoid_alpha * input2_rs
Shape Adaptor as a Learnable Down-Sampling Layer
In the following figure, we illustrate how shape adaptor can be incorporated into two commonly used down-sampling computational modules: a convolutional cell in VGG-like neural networks, and a residual cell in ResNet-like neural networks. To seamlessly insert shape adaptors into human-designed networks, we build shape adaptors on top of the same sampling functions used in the original network design. For example, in a single convolutional cell, we apply max-pooling as the down-sampling layer, and the identity layer is simply an identity mapping. And in a residual cell, we use the 'shortcut' $[1\times 1]$ convolutional layer as the down-sampling layer, and the weight layer stacked with multiple convolutional layers as the identity layer. In the ResNet design, we double the scaling weights in the residual cell, in order to match the same feature scale as in the original design.
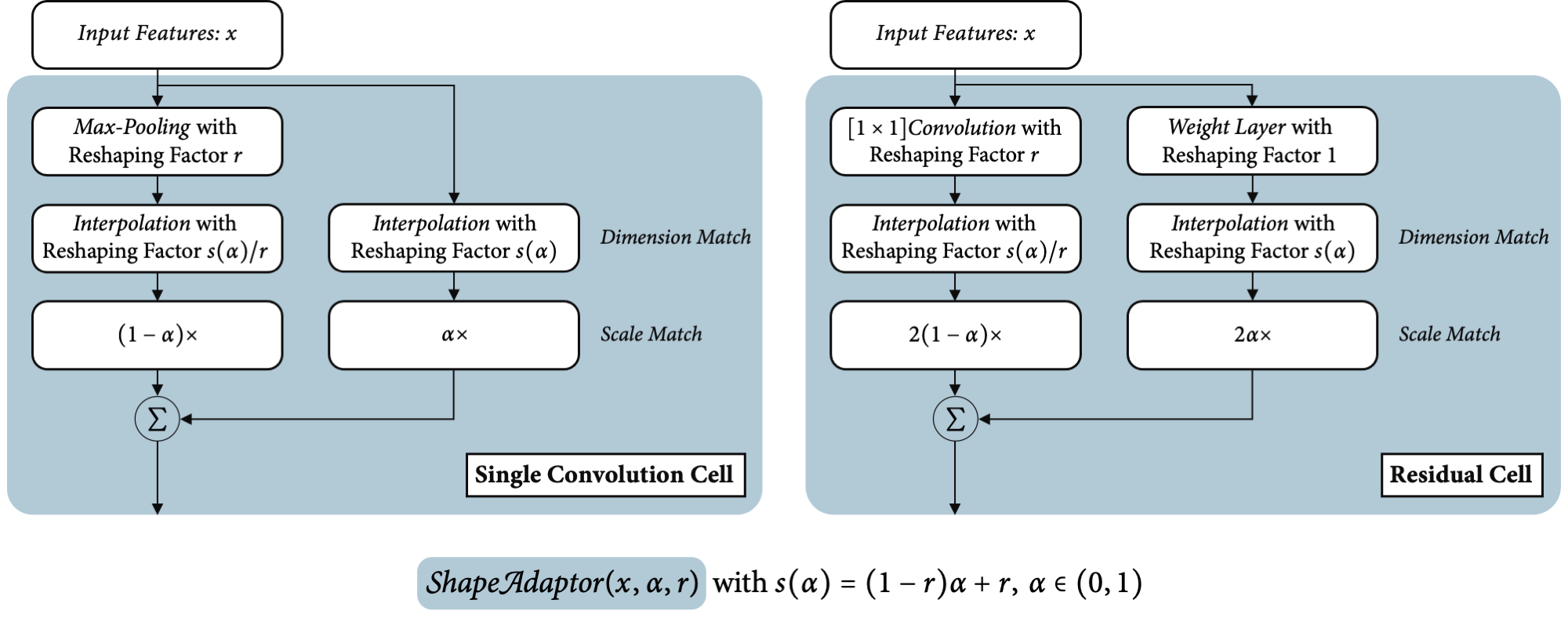
Visualisation of a down-sampling shape adaptor built on a convolutional
cell and a residual cell with a reshaping factor in the range (r, 1).
Experiments
Results on Image Classification Datasets
First, we compared networks built with shape adaptors to the original human-designed networks, to test whether shape adaptors can improve performances solely by finding a better network shape, without using any additional parameter space. To ensure fairness, all network weights in the human-designed and shape adaptor networks were optimised using the same hyper-parameters, optimiser, and scheduler.
| Dataset |
VGG-16 |
ResNet-50 |
MobileNetv2 |
| Human Designed |
Shape Adaptor |
Human Designed |
Shape Adaptor |
Human Designed |
Shape Adaptor |
| CIFAR-10 |
94.11 |
95.35 |
95.50 |
95.48 |
93.71 |
93.86 |
| CIFAR-100 |
75.39 |
79.16 |
78.53 |
80.29 |
73.80 |
75.74 |
| SVHN |
96.26 |
96.89 |
96.74 |
96.84 |
96.50 |
96.86 |
| ImageNet |
73.92 |
73.53 |
77.18 |
78.74 |
71.72 |
73.32 |
Top-1 test accuracies on different datasets for networks equipped with human-designed resizing layers and with shape adaptors. See more results in the original publication.
The table above shows the test accuracies of shape adaptor and human-designed networks, with each
accuracy averaged over three individual runs. We see that in nearly all cases, shape adaptor
designed networks outperformed human-designed networks by a significant margin, despite both methods using exactly the same parameter space.
Robustness on Number of Shape Adaptors
In the figure below, we present visualisations of network shapes in human-designed and shape adaptor designed networks. We can see that the network shapes designed by our shape adaptors
are visually similar even when different numbers of shape adaptor modules are used. In Aircraft
dataset, we see a narrower shape with MobileNetv2 due to inserting an excessive number
of 10 shape adaptors, which eventually converged to a local minima and lead to a degraded
performance.

Visualisation of human-designed and shape adaptor designed network shapes.
The number on the second row represents the number of resizing layers (or shape adaptors)
applied in the network.
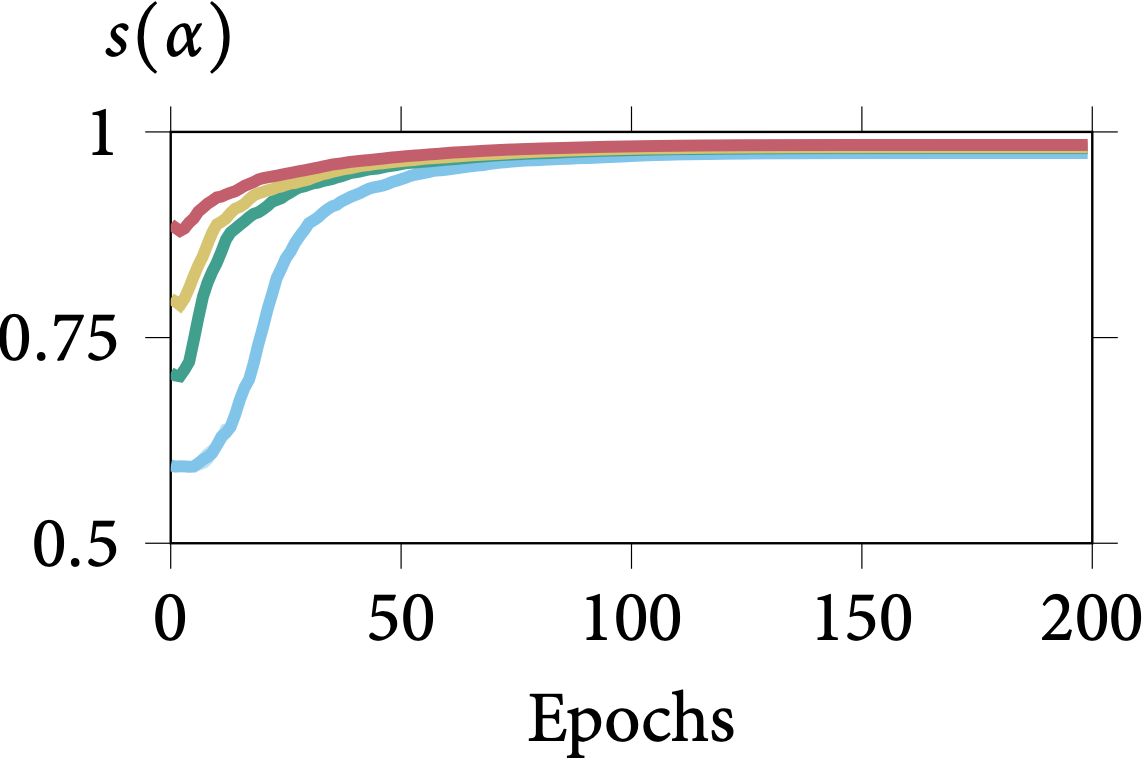
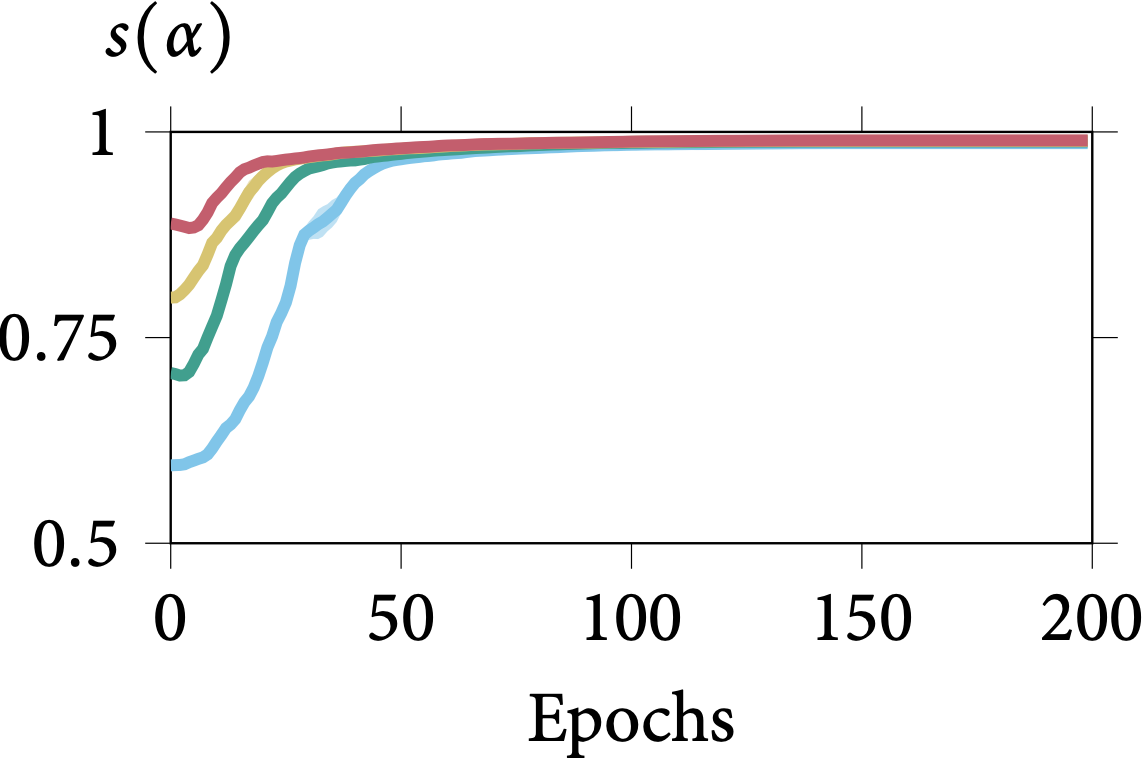
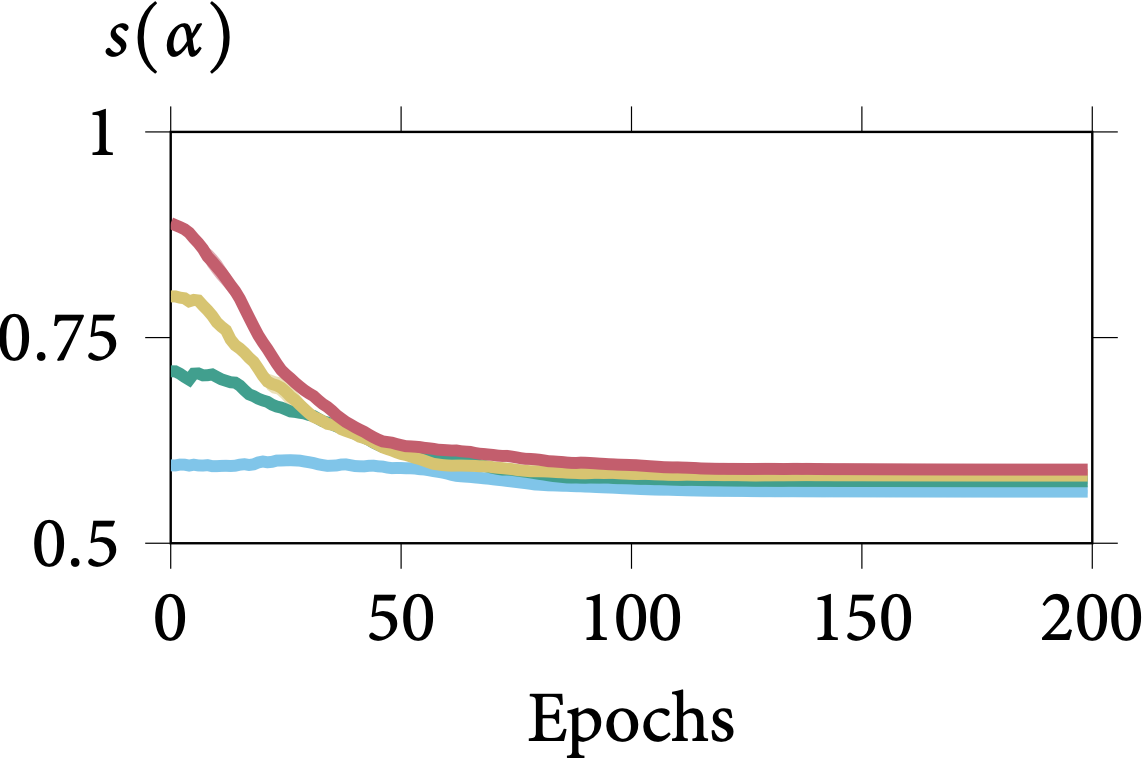
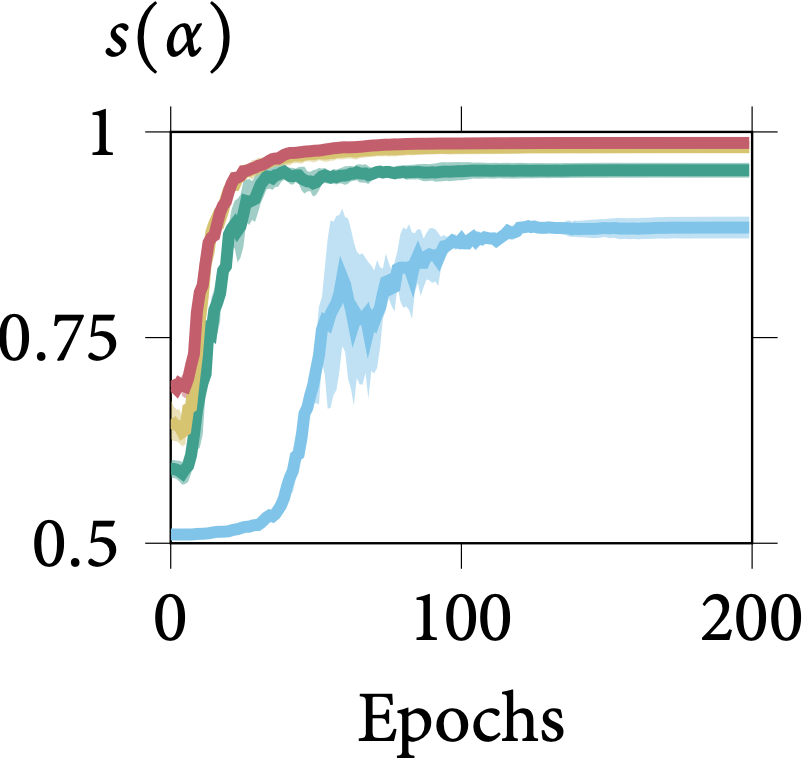
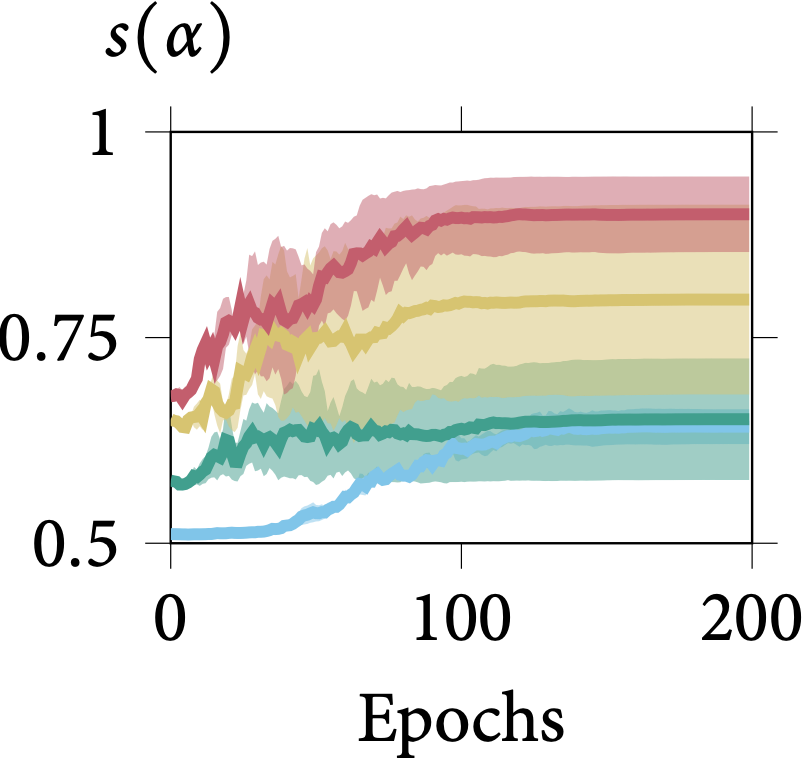
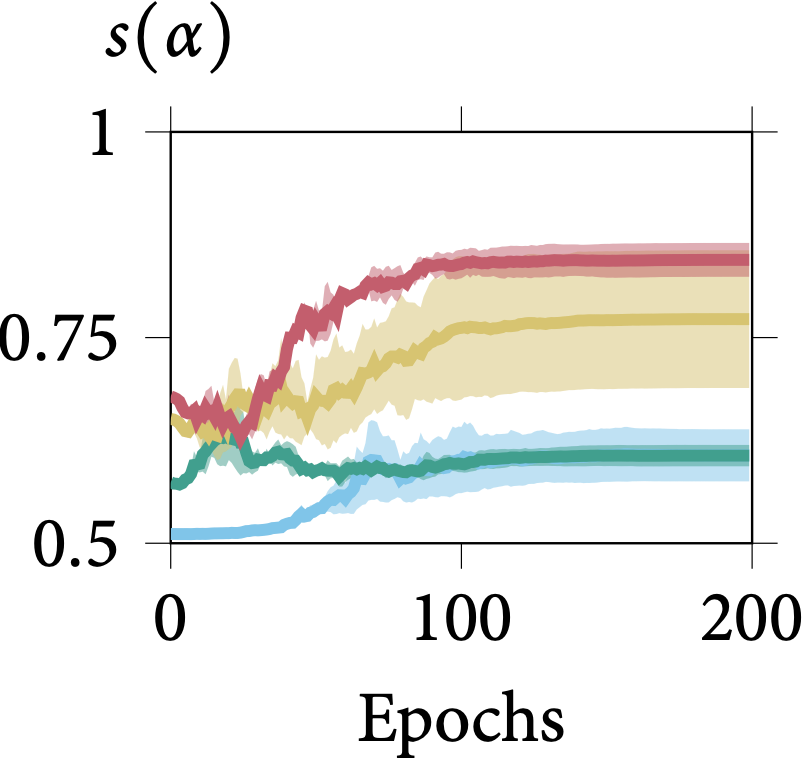
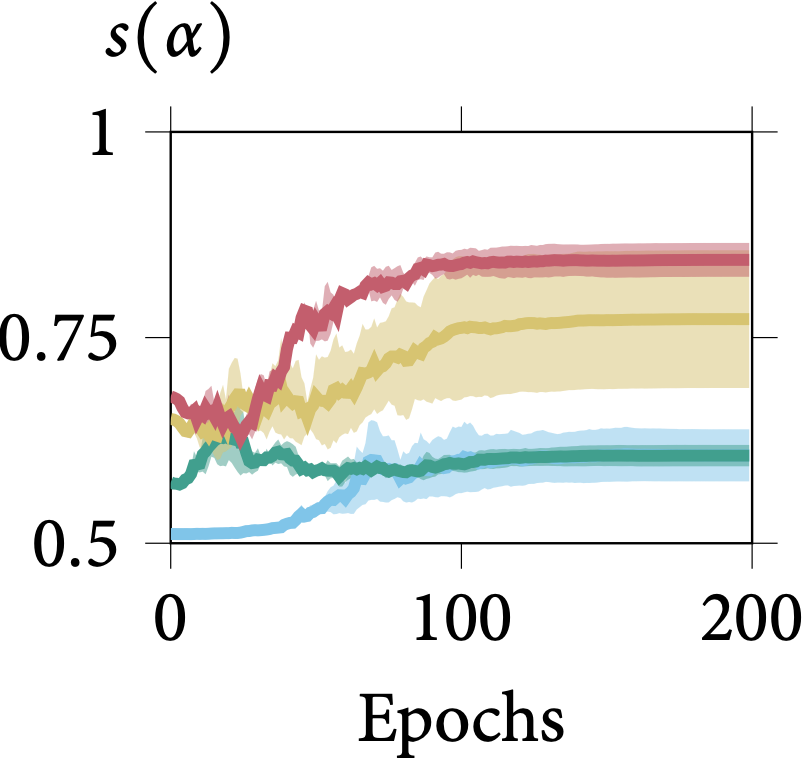
Robustness on Shape Adaptor Initialisation
In the following figure, we present the learning dynamics for each shape adaptor module across the entire training stage. We can observe that shape adaptors are learning in an almost identical pattern across different initialisations in the CIFAR-100 dataset, with nearly no variance. For
the larger resolution Aircraft dataset, different initialised shape adaptors converged to a different local minimum. They still follow a general trend, for which the reshaping factor of a
shape adaptor inserted in the deeper layers would converge into a smaller scale.
A detailed Study on Neural Shape Learning
In order to further understand how network performance is correlated with different network shapes, we ran a large-scale experiment by training 200 VGG-16 networks with randomly generated shapes.

In the figure above, we visualise the randomly generated network shapes with the best and the worst performance, and compare them to the network shapes in human designed and shape adaptor networks.
First, we can see that the best randomly searched shape obtains a very similar performance as well as a similar structure of shape compared to the ones learned from shape adaptors. Second, the reshaping factors in the worst searched shape are arranged from small to large, which is the direct opposite trend to the reshaping factors automatically learned by our shape adaptors. Third, human-designed networks are typically under-sized, and just by increasing network memory cost is not able to guarantee an improved performance. Finally, we can see a clear correlation between memory cost and performance, where a higher memory cost typically increases performance. However, this correlation ceases after 5G of memory consumption, after which point we see no improved performance. Interestingly, the memory cost of shape adaptors lies just on the edge of this point, which again shows the shape adaptor's ability to learn optimal design.
Other Applications
In this section, we present two additional applications of shape adaptors: Automated Shape
Compression (AutoSC) and Automated Transfer Learning (AutoTL).
Automated Shape Compression (AutoSC)
In AutoSC, we show that shape adaptors can also achieve strong results, when automatically finding optimal memory-bounded network shapes based on an initial human design. Instead of the original implementation of shape adaptors where these are assumed to be the only resizing layers in the network, with AutoSC we attach downsampling shape adaptors only on top of the non-resized layers of the human-designed architecture, whilst keeping the original human-designed resizing layers unchanged. Here, we insert global type shape adaptors, to be initialised so that the network shape is identical to the human-designed architecture, and thus the down-sampling shape adaptors can only earn to compress the network shape. This guarantees that the learned shape requires no more memory than the human-designed shape.
| 200/300M MobileNetv2 |
#Params |
MACs |
Acc. |
| Human 0.75 × |
2.6M |
233M |
69.8 |
| AutoSC 0.85 × |
2.9M |
262M |
70.7 |
| Human 1.0 × |
3.5M |
330M |
71.8 |
| AutoSC 1.1 × |
4.0M |
324M |
72.3 |
| Plain MobileNetv2 |
#Params |
MACs |
Acc. |
| Human 1.0 × |
2.3M |
94.7M |
73.80 |
| AutoSC 1.0 × |
2.3M |
91.5M |
74.81 |
| Human 1.0 × |
2.3M |
330M |
77.64 |
| AutoSC 1.0 × |
2.3M |
326M |
78.95 |
Test accuracies for AutoSC and human-designed MobileNetv2 on CIFAR-100, Aircraft, and ImageNet. × represents the applied width multiplier.
In the table above, we present AutoSC built on MobileNetv2, an efficient network design for mobile applications. We evaluate AutoSC on three datasets: CIFAR-100, Aircraft and ImageNet. During training of MobileNetv2, we initialised a small width multiplier on the network's channel dimension to slightly increase the parameter space (if applicable). By doing this, we ensure that this wider network after compression would have a similar memory consumption as the human-designed MobileNetv2, for a fair comparison. In all three datasets, we can observe that shape adaptors are able to improve performance, despite having similar memory consumption compared to human-designed networks.
Automated Transfer Learning (AutoTL)
In this section, we present how shape adaptors can be used to perform transfer learning in
an architectural level. In AutoTL, we directly replace the human-designed resizing layers
with shape adaptors, and initialise them with the reshaping factors designed in the original
human-defined architecture, to match the spatial dimension of each pre-trained network
layer. During fine-tuning, the network is then fine-tuning with network weights along with
network shapes, thus improving upon the standard fine-tuning in a more flexible manner.
| Method |
Bird |
Cars |
Flowers |
WikiArt |
Skethes |
| PackNet |
80.41 |
86.11 |
93.04 |
69.40 |
76.17 |
| PiggyBack |
81.59 |
89.62 |
94.77 |
71.33 |
79.91 |
| NetTailor |
82.52 |
90.56 |
95.79 |
72.98 |
80.48 |
| Fine-tune |
81.86 |
89.74 |
93.67 |
75.60 |
79.58 |
| SpotTune |
84.03 |
92.40 |
96.34 |
75.77 |
80.20 |
| AutoTL |
84.29 |
93.66 |
96.22 |
77.47 |
80.74 |
Test accuracies of transfer Learning methods built on ResNet-50 on fine-grained
datasets.
The results for AutoTL and other state-of-the-art transfer learning methods are listed here, for which we outperform 4 out of 5 datasets. The most related methods to our approach
are standard fine-tuning and SpotTune, which optimise the entire network parameters for
each dataset. Other approaches like PackNet, Piggyback, and NetTailor focus
on efficient transfer learning by updating few task-specific weights. We design AutoTL with
standard fine-tuning, as the simplest setting to show the effectiveness of shape adaptors. In
practice, AutoTL can be further improved, and integrated into other efficient transfer learning
techniques.
Conclusions & Future Directions
In this paper, we present shape adaptor, a learnable resizing module to enhance existing
neural networks with task-specific network shapes. With shape adaptors, the learned network shapes can further improve performances compared to human-designed architectures, without requiring in increase in parameter space. We show that shape adaptors are robust to hyper-parameters, and typically learn very similar network shapes, regardless of the number of shape adaptor modules used. In addition, we show that shape adaptors can also be easily incorporated into other applications, such as network compression and transfer learning.
In future work, we will investigate shape adaptors in a multi-branch design, where the formulation provided in this paper extended to integrating more than two resizing layers in
each shape adaptor module. Due to the success of shape adaptors in the other applications
we have presented in this paper, we will also study use of shape adaptors for more applications, such as neural architecture search, and multi-task learning.
Citation
If you found this work is useful in your own research, please considering citing the following.
@inproceedings{liu2020shape_adaptor,
title={Shape Adaptor: A Learnable Resizing Module},
author={Liu, Shikun and Lin, Zhe and Wang, Yilin and Zhang, Jianming and Perazzi, Federico and Johns, Edward},
booktitle={Proceedings of the European Conference on Computer Vision (ECCV)},
year={2020}
}