Auxiliary learning is a method to improve the ability of a primary task to generalise to unseen data, by training on additional auxiliary tasks alongside this primary task. The sharing of features across tasks results in additional relevant features being available, which otherwise would not have been learned from training only on the primary task. Auxiliary learning is similar to multi-task learning, except that only the performance of the primary task is of importance, and the auxiliary tasks are included purely to assist the primary task.
Auxiliary learning methods can be mainly divided into two main directions:
Supervised auxiliary learning: Suitable auxiliary tasks can be manually chosen to complement the primary tasks, but requiring the domain knowledge to choose the auxiliary tasks and labelled data to train the auxiliary tasks.
Unsupervised auxiliary learning: It removes the need for labelled data, but at the expense of a limited set of auxiliary tasks which may not be beneficial for the primary task.
By combining the merits of both supervised and unsupervised auxiliary learning, the ideal framework would be one with the flexibility to automatically determine the optimal auxiliary tasks, but without the need to manually label these auxiliary tasks.
We propose to achieve such a framework with a simple and general meta-learning algorithm, which we call Meta AuXiliary Learning (MAXL). We first observe that in supervised learning, defining a task can equate to defining the labels for that task. Therefore, for a given primary task, an optimal auxiliary task is one which has optimal labels. The goal of MAXL is then to automatically discover these auxiliary labels using only the labels for the primary task.
Before we introduce the design of MAXL, we first performed an empirical analysis to study the generalisation based on different auxiliary tasks. In this project, both the primary and auxiliary tasks are considered to be image classification for simplicity, and here the empirical analysis is performed on a 4-level CIFAR-100 dataset, with the design details shown in the following table.
| 3 Class | 10 Class | 20 Class | 100 Class |
|---|---|---|---|
| animals | large animals | reptiles | crocodile, dinosaur, lizard, snake, turtle |
| large carnivores | bear, leopard, lion, tiger, wolf | ||
| large omnivores and herbivores | camel, cattle, chimpanzee, elephant, kangaroo | ||
| medium animals | aquatic mammals | beaver, dolphin, otter, seal, whale | |
| medium-sized mammals | fox, porcupine, possum, raccoon, skunk | ||
| small animals | small mammals | hamster, mouse, rabbit, shrew, squirrel | |
| fish | aquarium fish, flatfish, ray, shark, trout | ||
| invertebrates | insects | bee, beetle, butterfly, caterpillar, cockroach | |
| non-insect invertebrates | crab, lobster, snail, spider, worm | ||
| people | people | baby, boy, girl, man, woman | |
| vegetations | vegetations | flowers | orchids, poppies, roses, sunflowers, tulips |
| fruit and vegetables | apples, mushrooms, oranges, pears, peppers | ||
| trees | maple, oak, palm, pine, willow | ||
| objects and scenes | household objects | food containers | bottles, bowls, cans, cups, plates |
| household electrical devices | clock, keyboard, lamp, telephone, television | ||
| household furniture | bed, chair, couch, table, wardrobe | ||
| construction | large man-made outdoor things | bridge, castle, house, road, skyscraper | |
| natural scenes | large natural outdoor scenes | cloud, forest, mountain, plain, sea | |
| vehicles | vehicles 1 | bicycle, bus, motorcycle, pickup truck, train | |
| vehicles 2 | lawn-mower, rocket, streetcar, tank, tractor |
CIFAR-100 dataset in a 4-level hierarchy. The original dataset is consisted of 20 (coarse) labels and 100 (fine) labels. And we additionally added 2 additional coarse levels with 3 and 10 labels.
We first exhaustively run experiments, training a different set of primary and auxiliary tasks using the human-defined labels in the table above. Results are shown in the following figures.




Validation accuracy of the primary task trained with different auxiliary tasks.
From these results, we may conclude with some interesting observations on auxiliary learning. Note that these observations are only true based on the fact that both primary and auxiliary tasks are of the same type -- in this example -- image classification.
Observation #1: The performance of the primary task will improve only if we train with an auxiliary task with a higher information entropy. (from the results in the first row)
Observation #2: The improved performance of the primary task only depends on the optimal auxiliary task alone, independent of additional non-optimal auxiliary tasks. (from the results in the second row)
Here, the information entropy is measured by the number of labels in the prediction space, i.e., a larger number (finer level) of label space has higher information entropy. To learn beyond the information limited by the same type of tasks, a more optimal auxiliary learning framework is to combine the information brought by a diverse set of auxiliary tasks of different types, automatically filter the right information based on the choice of the primary tasks, which motivates to our recent project Auto-Lambda.
Considering image classification as the primary task, the auxiliary task is then defined as a sub-class labelling problem. Based on the observations listed in the previous section, we associate each primary class with a number of auxiliary classes, in a two-level hierarchy, and learn a single optimal auxiliary task with this pre-defined hierarchy. For example, if manually-defined labels were used, a primary class could be "Dog", and one of the auxiliary classes could be "Border Collie". Except in our case, the concept of "Border Collie" is automatically generated by MAXL. The goal of MAXL is to generate these labels for the auxiliary task which, when trained alongside a primary task, improve the performance of the primary task.
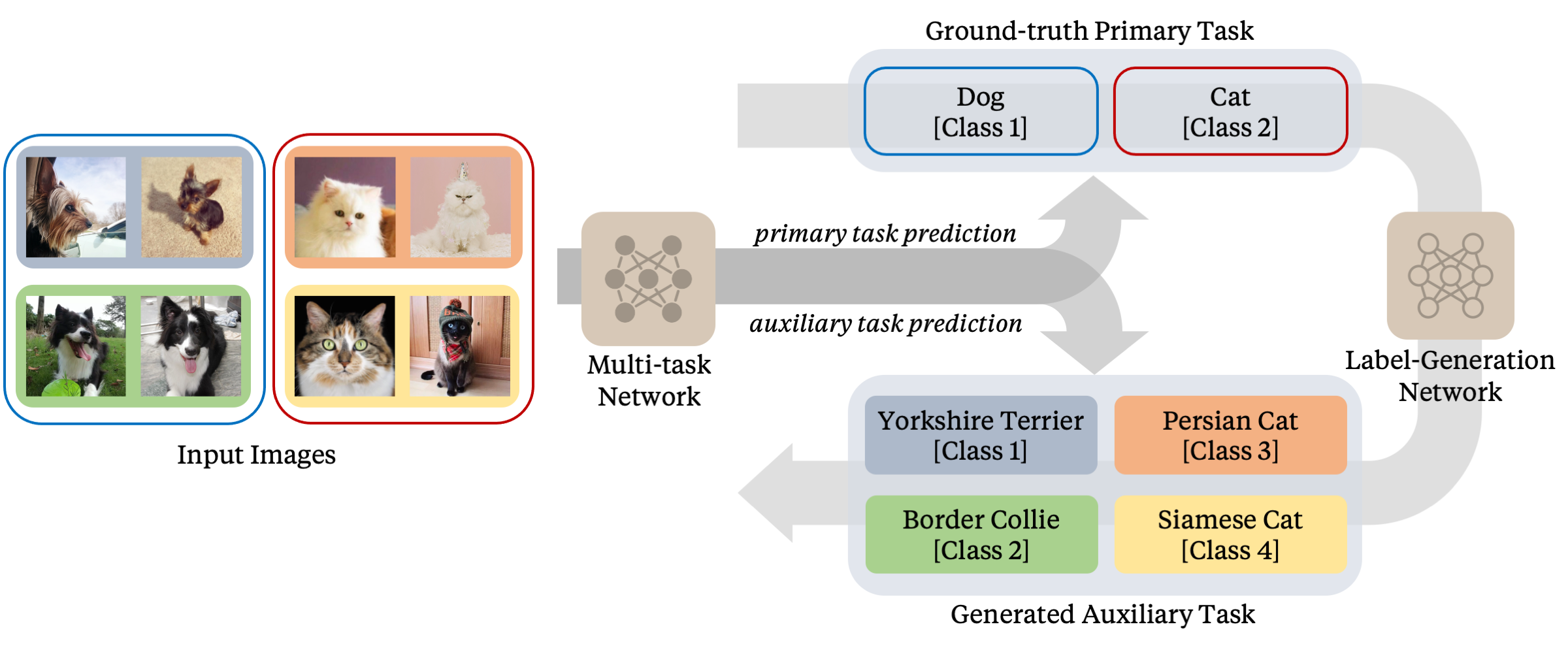
The overview of MAXL framework. The performance of the primary task can be improved by training the primary task together with an auxiliary task defined by these generated auxiliary labels. Here, the auxiliary task is to divide each primary class into two sub-classes.
To accomplish this, we train two networks: a multi-task network, which trains on the primary and auxiliary task in a standard multi-task learning setting, and a label-generation network, which generates the labels for the auxiliary task.
We denote the multi-task network as a function $f_{\theta_1}(x)$ with parameters $\theta_1$ which takes an input $x$, and the label-generation network as a function $g_{\theta_2}(x)$ with parameters $\theta_2$ which takes the same input $x$. Parameters $\theta_1$ are updated by losses of both the primary and auxiliary tasks, as is standard in multi-task learning. However, $\theta_2$ is updated only by the performance of the primary task, as a form of gradient-based meta learning.
Update multi-task network parameters $\theta_1$: $$ \text{argmin}_{\theta_1}\left(\mathcal{L}(f^\text{pri}_{\theta_1}(x), y^\text{pri}) + \mathcal{L}(f^\text{aux}_{\theta_1}(x), y^\text{aux})\right) $$ Update label-generation network $\theta_2$: $$ \text{argmin}_{\theta_2}\mathcal{L}(f^\text{pri}_{\theta_1^+}(x), y^\text{pri}) $$ from which, $$ \theta_1^+ = \theta_1- \alpha\nabla_{\theta_1}\left(\mathcal{L}(f^\text{pri}_{\theta_1}(x), y^\text{pri}) + \mathcal{L}(f^\text{aux}_{\theta_1}(x), y^\text{aux})\right) $$
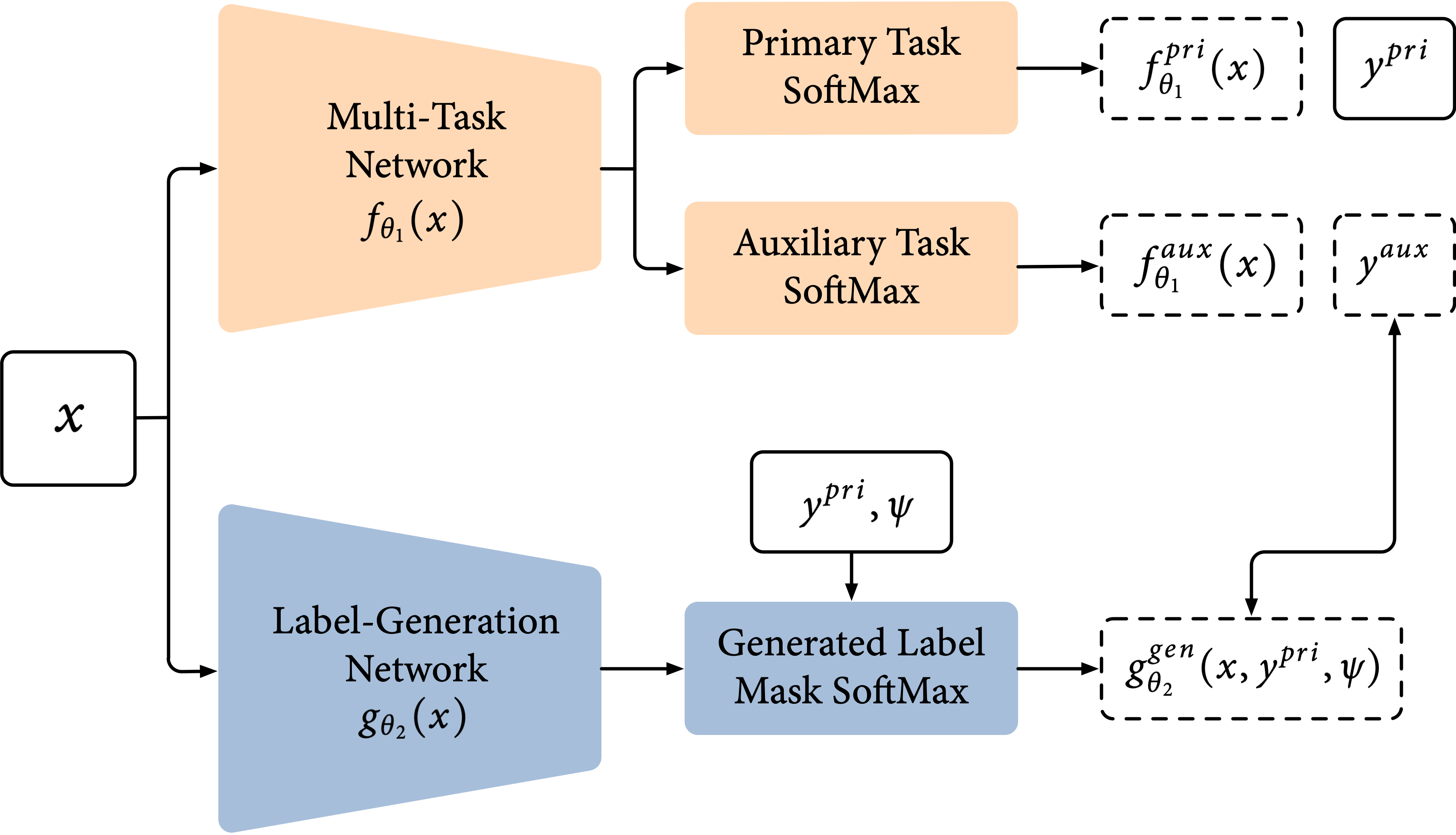
The trick in this second objective is that we perform a derivative over a derivative (a Hessian matrix) to update $\theta_2$, by using a retained computational graph of $\theta_1^+$, in order to compute derivatives with respect to $\theta_2$. This second-order gradients can also be approximated using finite difference, to reduce training speed, as used in differentiable architecture search.
As shown in Observation #1, the design of a useful auxiliary task should include a more number of labels than the one of the primary task. To achieve this, we include a hyper-parameter -- hierarchy $\psi$ which defines the number of auxiliary classes per primary class. To implement this, we designed a modified SoftMax function, which we call Mask SoftMax, to predict auxiliary labels only for certain auxiliary classes. This takes ground-truth primary task label $y$, and the hierarchy $\psi$, and creates a binary mask $M = B(y, \psi)$. The mask is zero everywhere, except for ones across the set of auxiliary classes associated with y.
For example, considering a primary task with 2 classes $y = 0, 1$, and a hierarchy of $\psi = [2, 2]$. In this case, the binary masks are $M = [1, 1, 0, 0]$ for $y = 0$, and $[0, 0, 1, 1]$ for $y = 1$. A visual illustration is shown below.
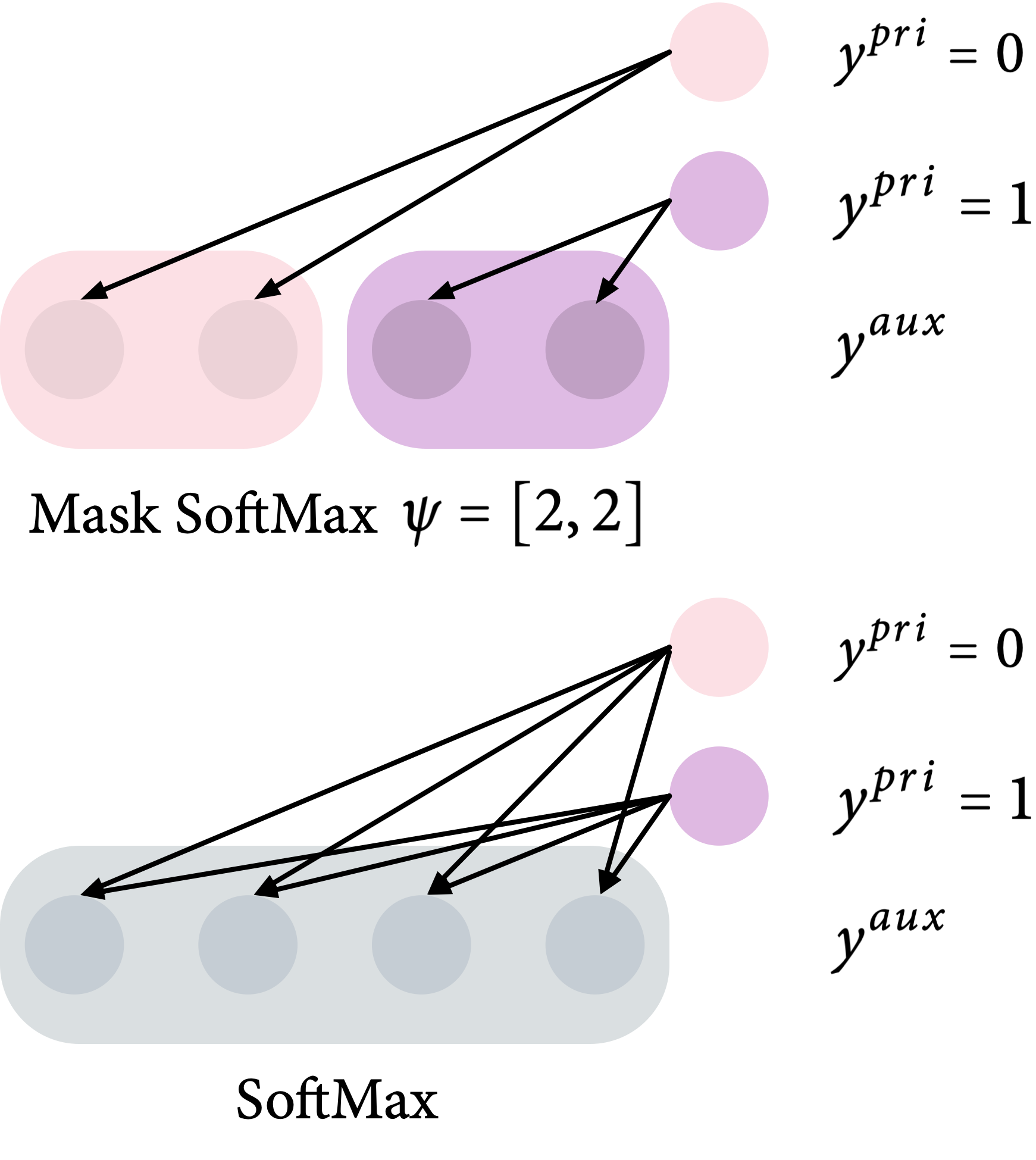
$$p(y_i) = \frac{\exp(M\cdot y_i)}{\sum_j \exp(M\cdot y_j)}$$
$$p(y_i) = \frac{\exp(y_i)}{\sum_j \exp(y_j)}$$
In addition, we found that the generated auxiliary labels can easily collapse, such that the label-generation network always generates the same auxiliary label, ignoring the designed hierarchy. Therefore, to encourage the network to learn more complex and informative auxiliary tasks, we further apply an entropy loss $\mathcal{H}(y^\text{aux})=y^\text{aux}\log y^\text{aux}$ as a regularisation term when updating $\theta_2$.
We compared MAXL to a number of baseline methods for generating auxiliary labels, on the 4-level CIFAR-100 dataset defined above:
Single Task: trains only with the primary class label and does not employ auxiliary learning.
Random: assigns each training image to random auxiliary classes in a randomly generated (well-balanced) hierarchy.
K-Means: determines auxiliary labels via unsupervised clustering using K-Means, performed on the latent representation of an auto-encoder.
Human: uses the human-defined hierarchy of CIFAR-100.
Here, all the baselines were trained without any regularisation, to isolate the effect of auxiliary learning and test generalisation ability purely from auxiliary tasks. And the results are shown in the following table.
| PRI 3 | AUX 10 | PRI 3 | AUX 20 | PRI 3 | AUX 100 | PRI 10 | AUX 20 | PRI 10 | AUX 100 | PRI 20 | AUX 100 | |
|---|---|---|---|---|---|---|
| Single | 87.49 | 87.49 | 87.49 | 75.15 | 75.15 | 79.71 |
| Random | 89.86 | 89.15 | 87.81 | 77.26 | 75.88 | 71.11 |
| K-Means | 90.16 | 90.57 | 90.43 | 77.68 | 78.63 | 73.35 |
| Human | 90.78 | 90.78 | 91.23 | 77.97 | 78.18 | 73.11 |
| MAXL | 90.59 | 90.68 | 90.61 | 78.64 | 78.43 | 74.28 |
Validation accuracy of the primary tasks trained with auxiliary tasks generated by different methods.
We observe that MAXL outperforms all baselines except Human. Note that K-Means required significantly longer training time than MAXL due to the need to run clustering after each iteration. Also note that the superior performance of MAXL over these three baselines occurs despite all four methods using exactly the same data. Finally, we observe that MAXL performs similarly to Human, despite this baseline requiring manually-defined auxiliary labels for the entire training dataset. With performance of MAXL similar to that of a system using human-defined auxiliary labels, we see strong evidence that MAXL is able to learn to generalise effectively in a self-supervised manner.
We further show examples of images assigned to the same auxiliary class through MAXL's label-generation network. Below shows example images with the highest prediction probabilities for 3 auxiliary classes on MNIST.
Auxiliary Class #1
Auxiliary Class #2
Auxiliary Class #3
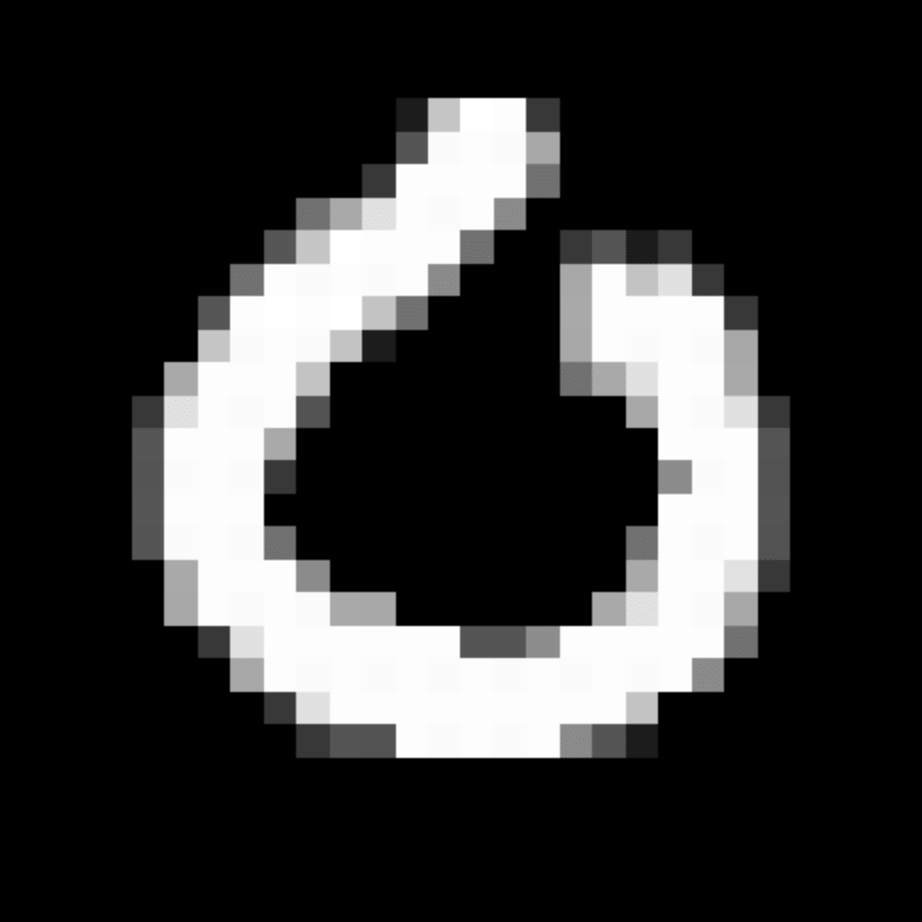

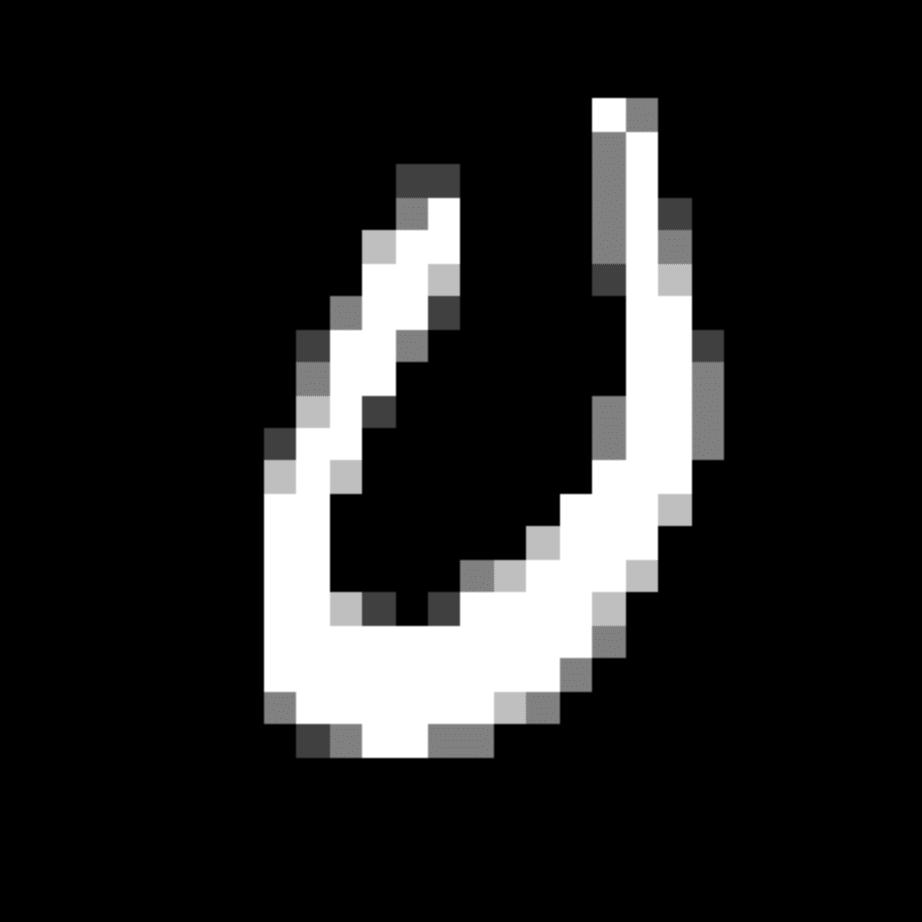
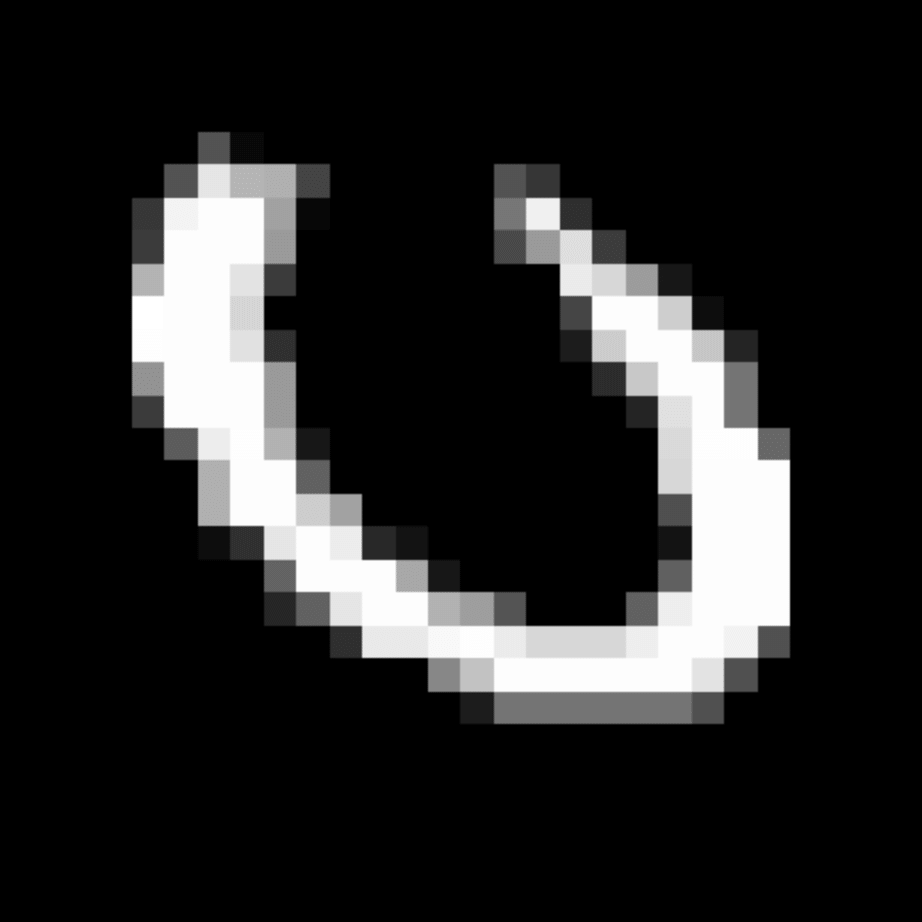

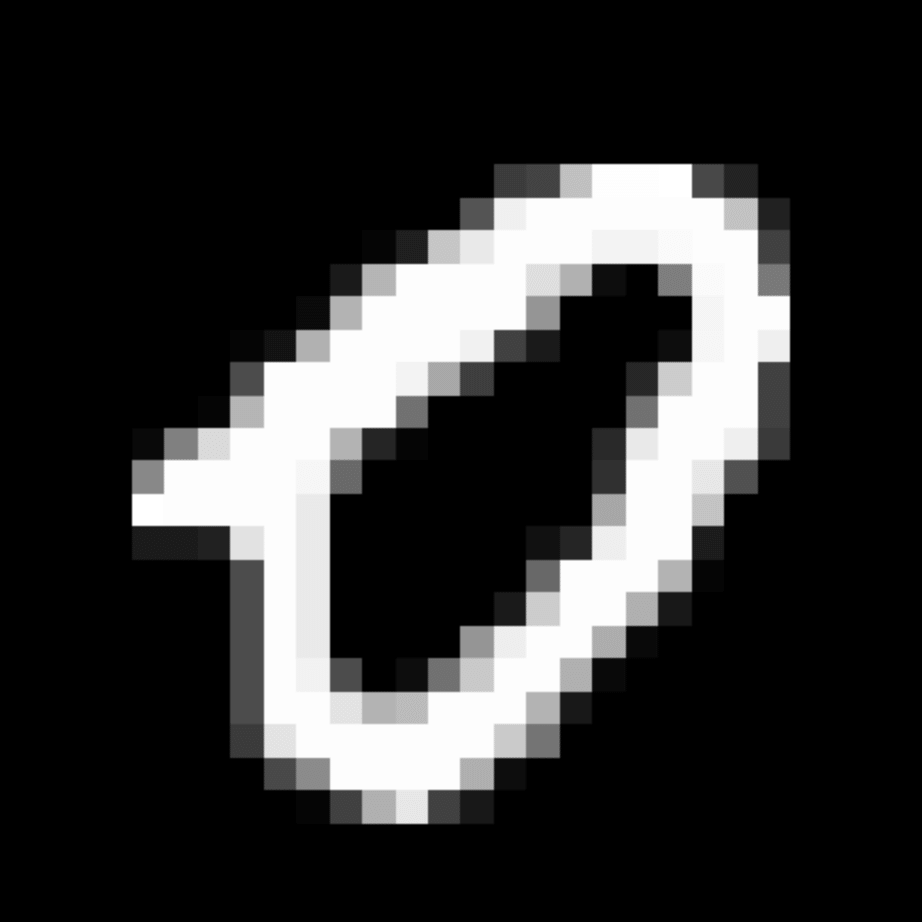
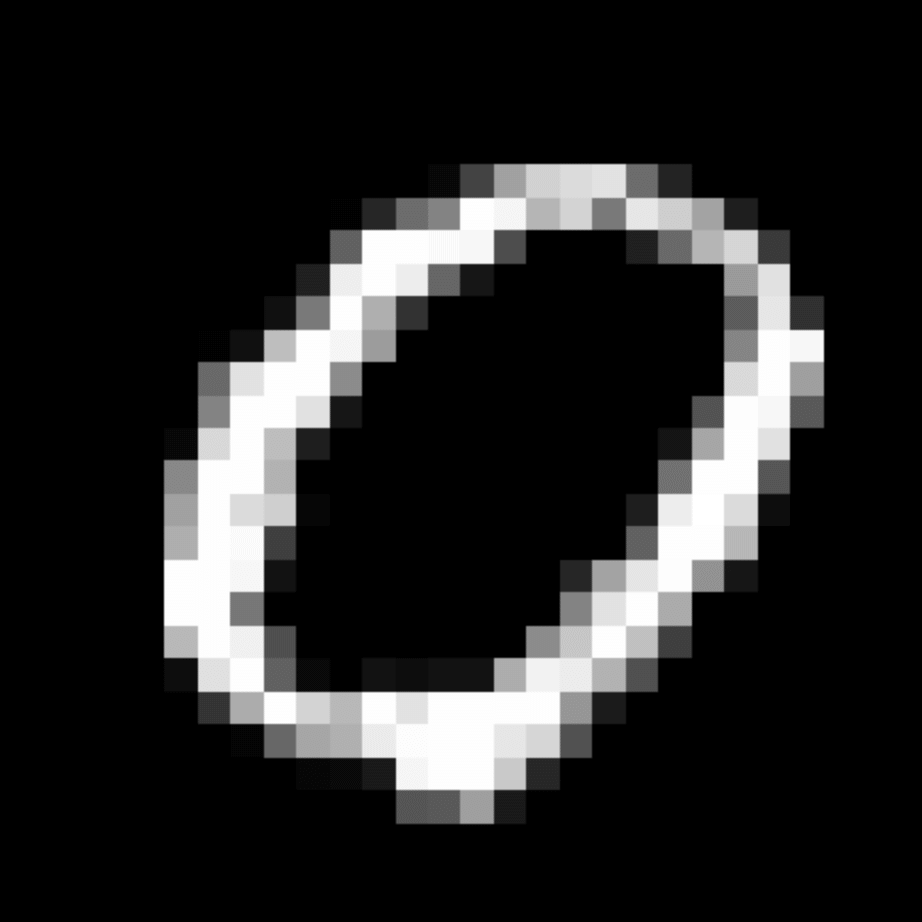

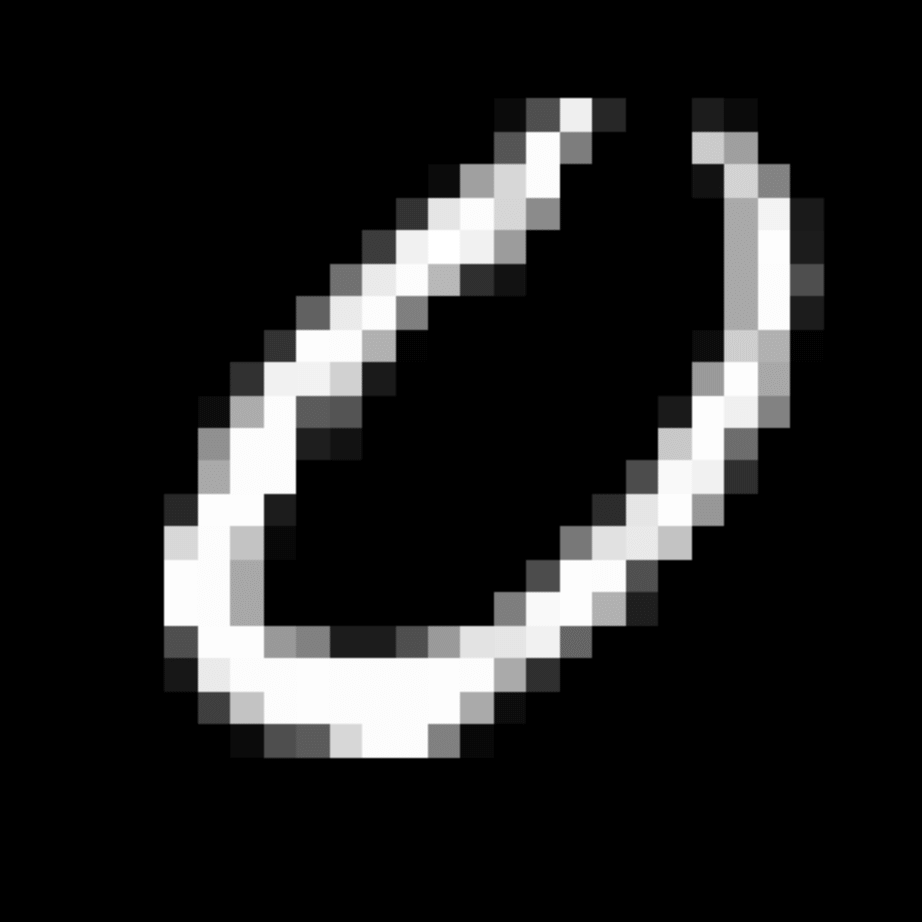
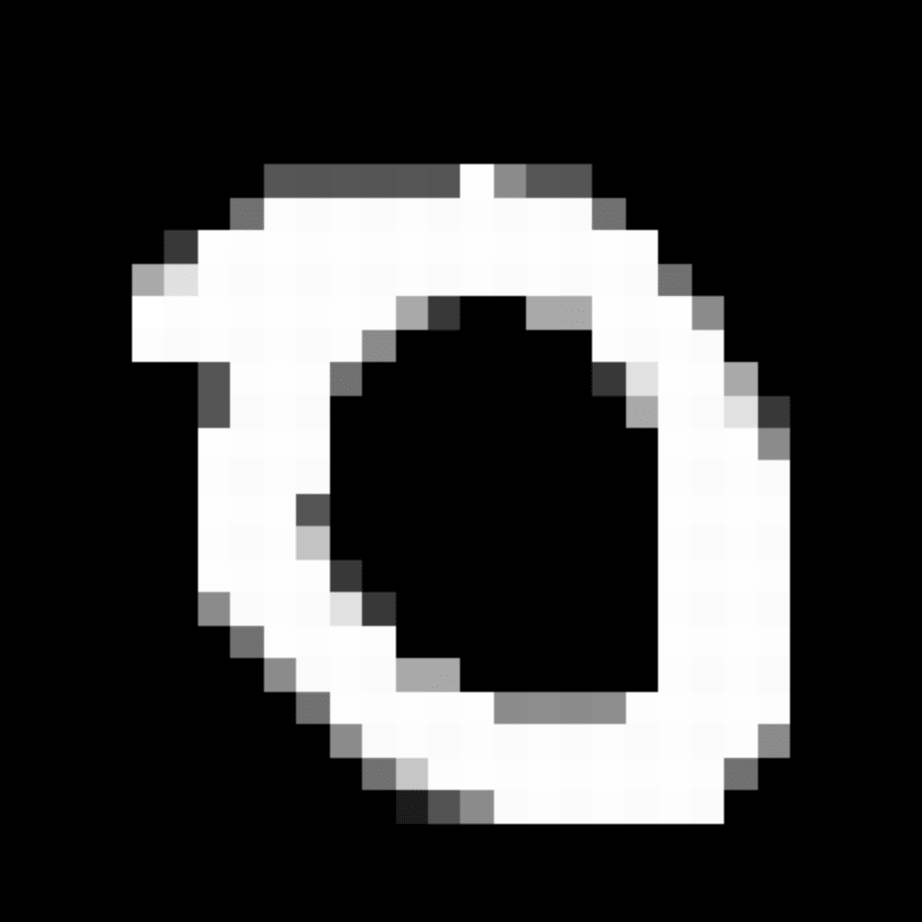
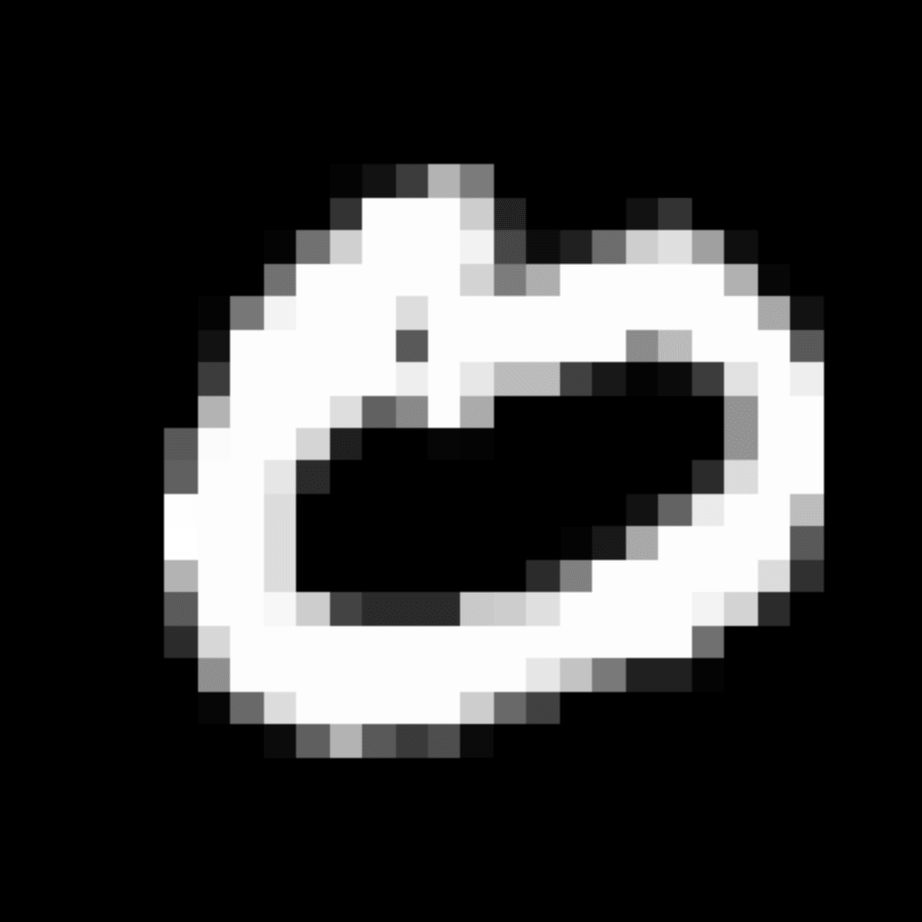
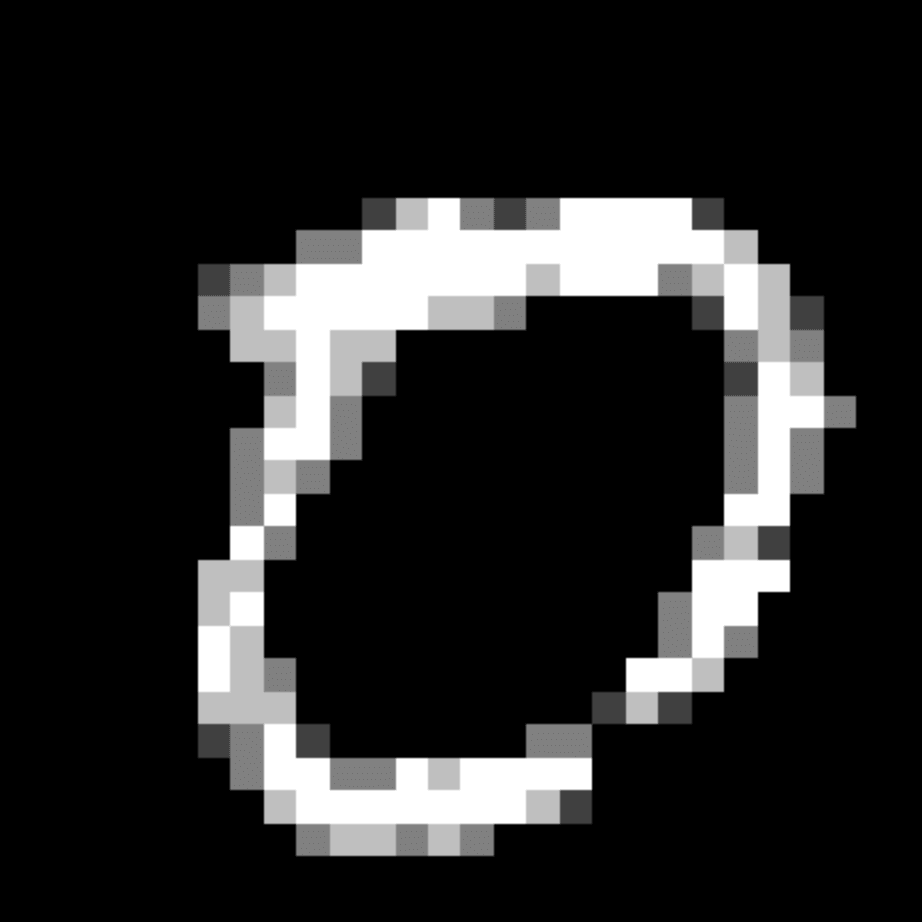
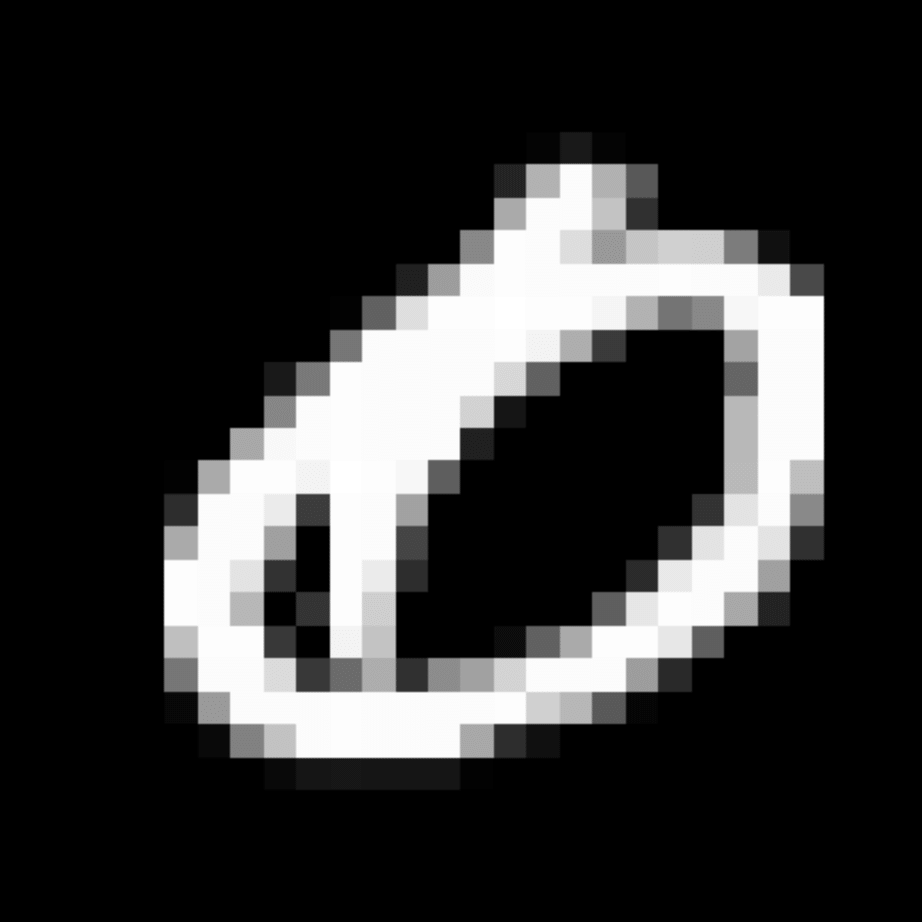
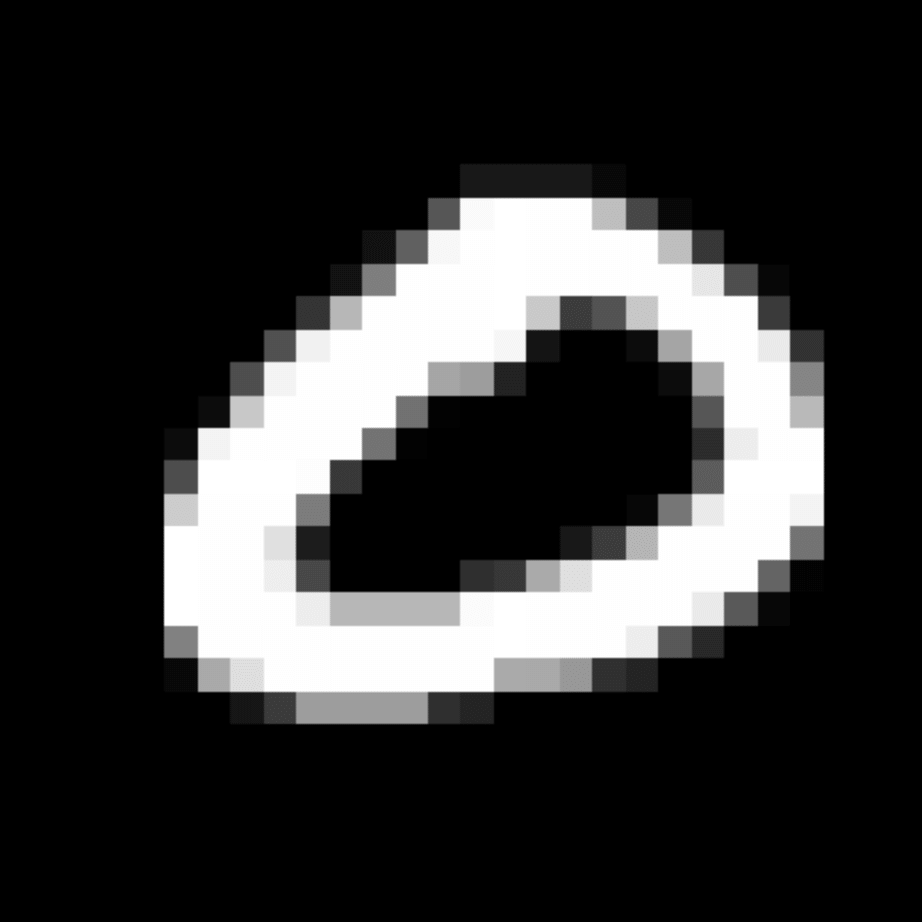

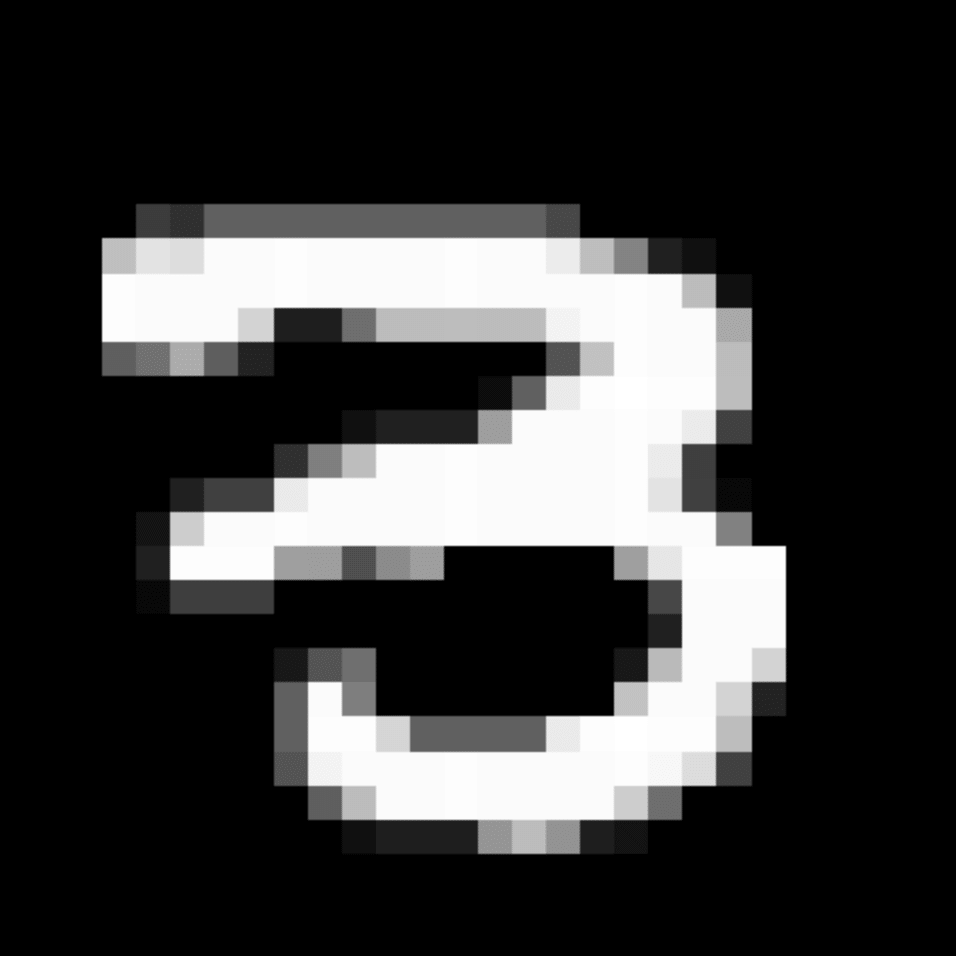
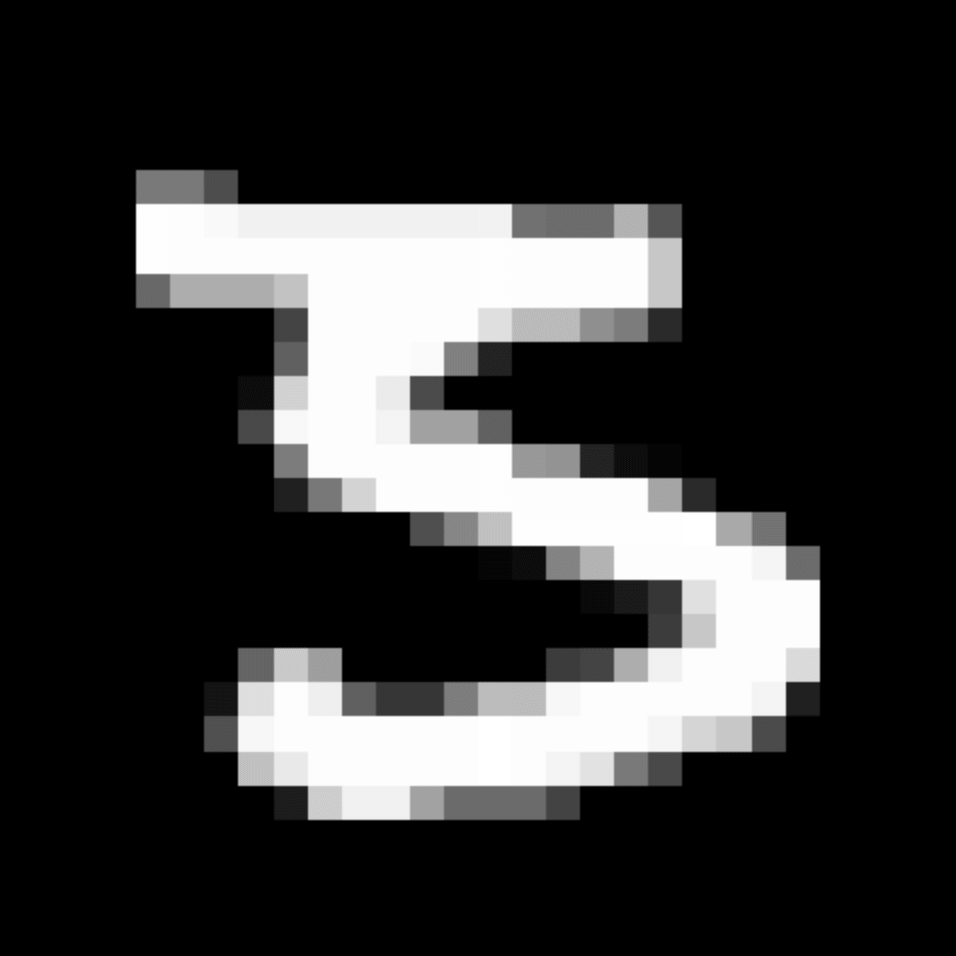
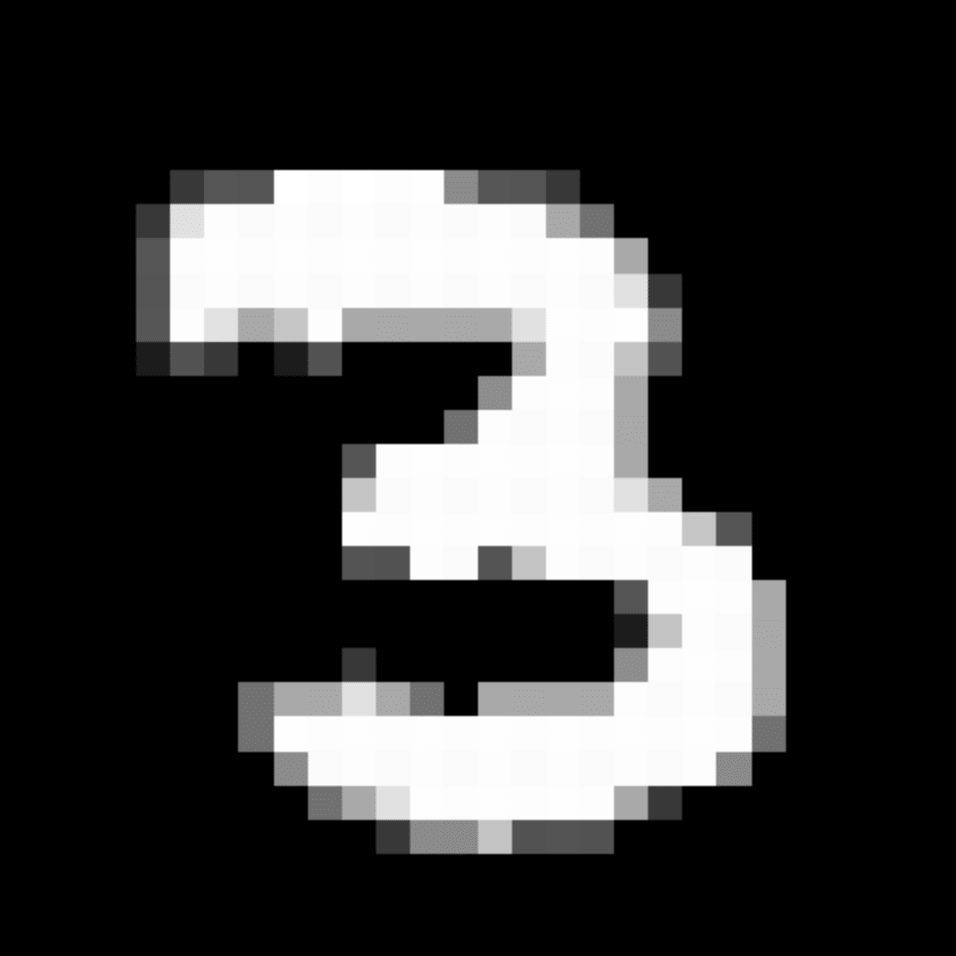
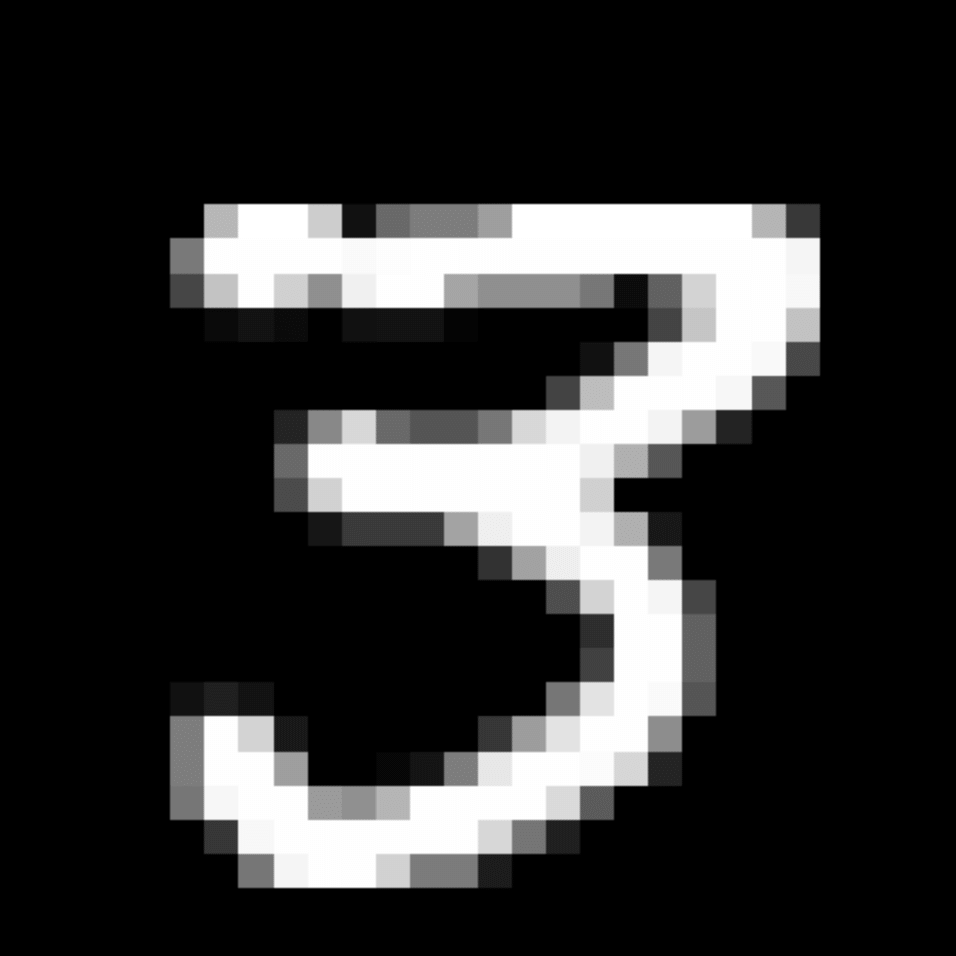
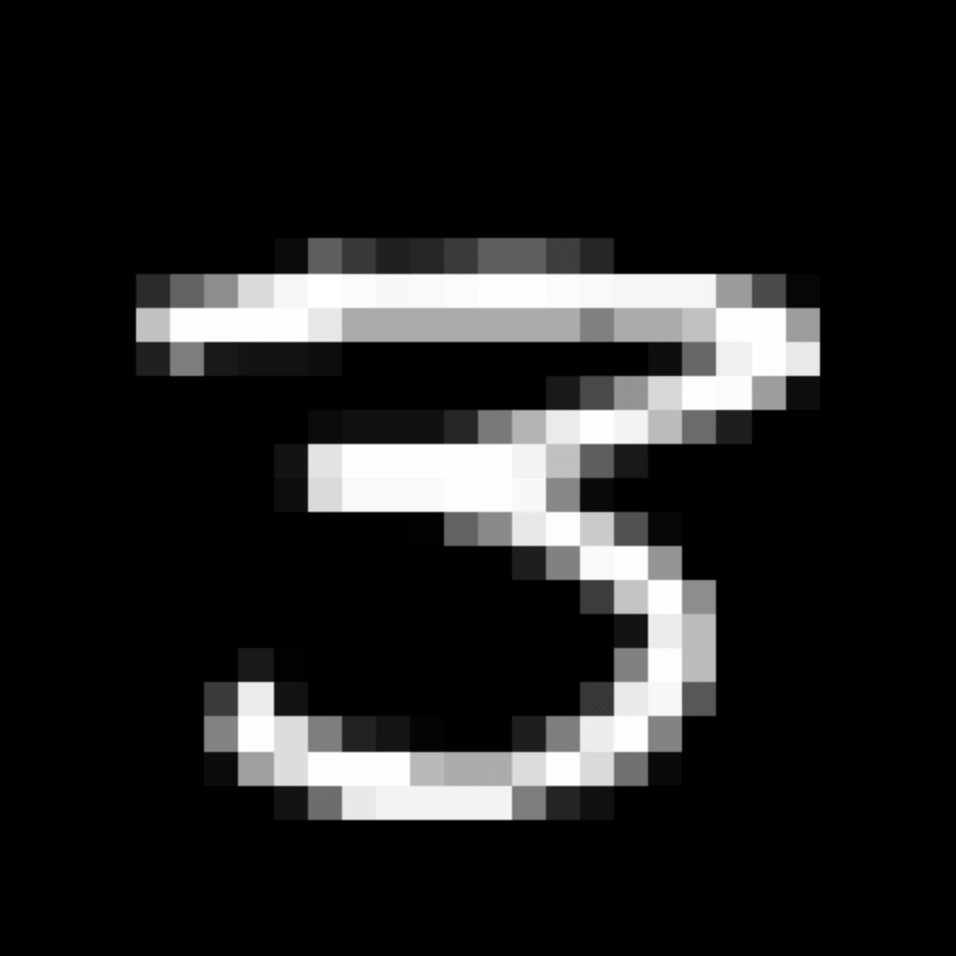
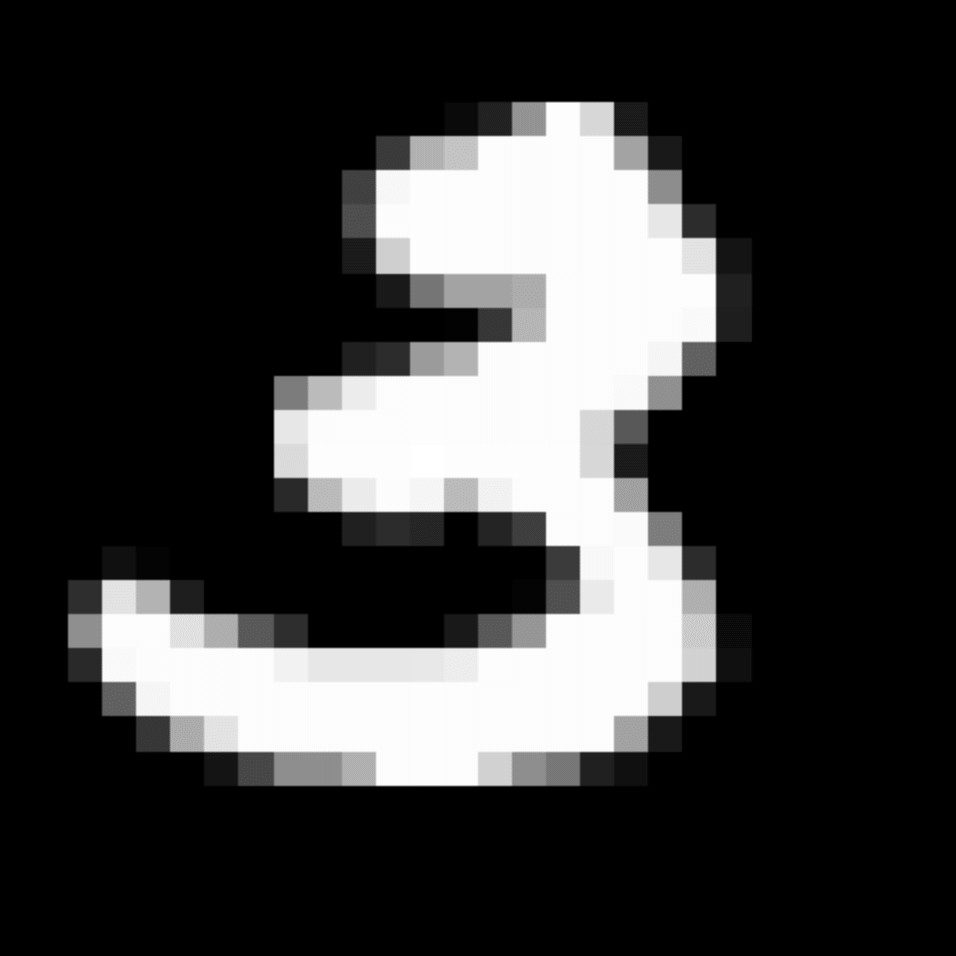
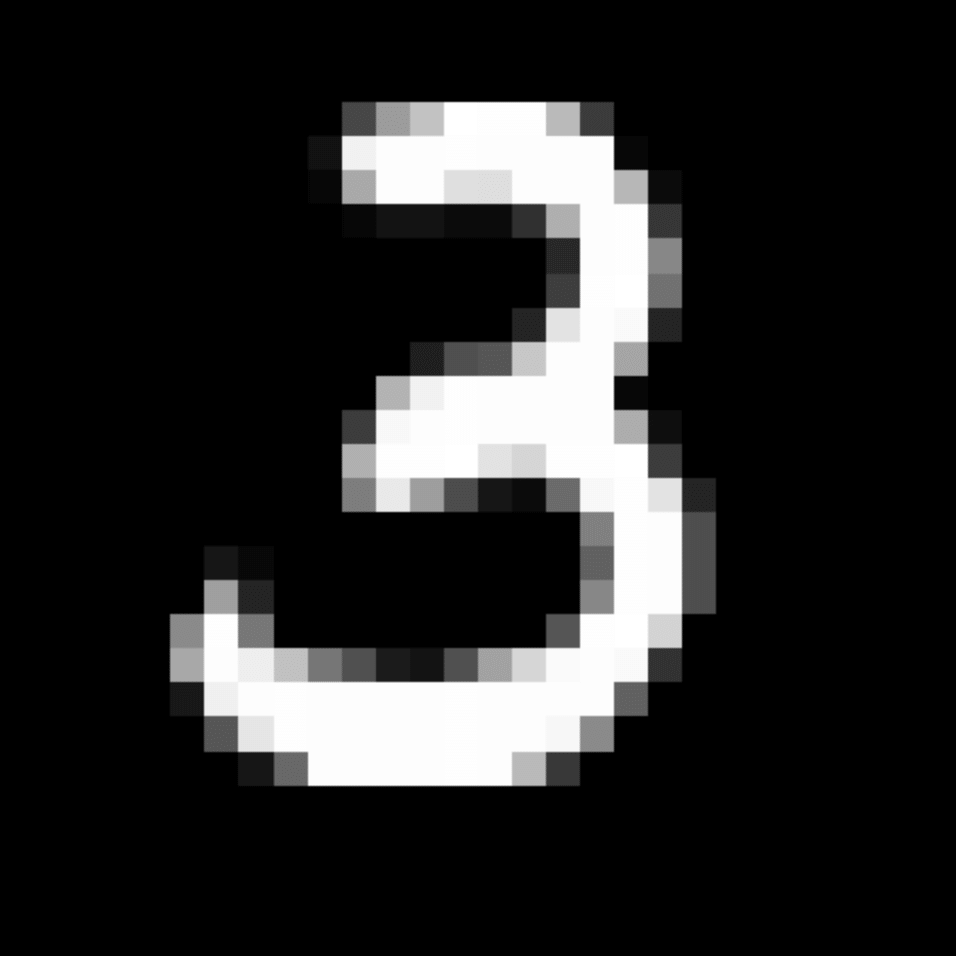
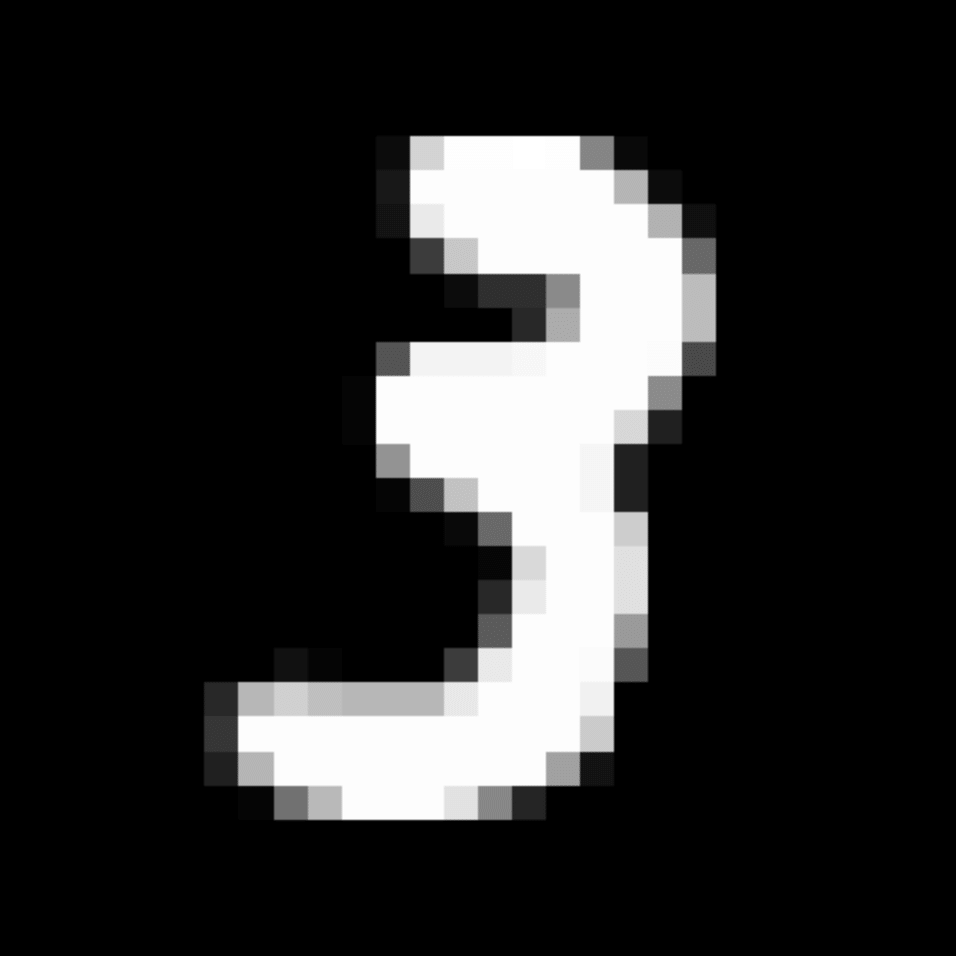
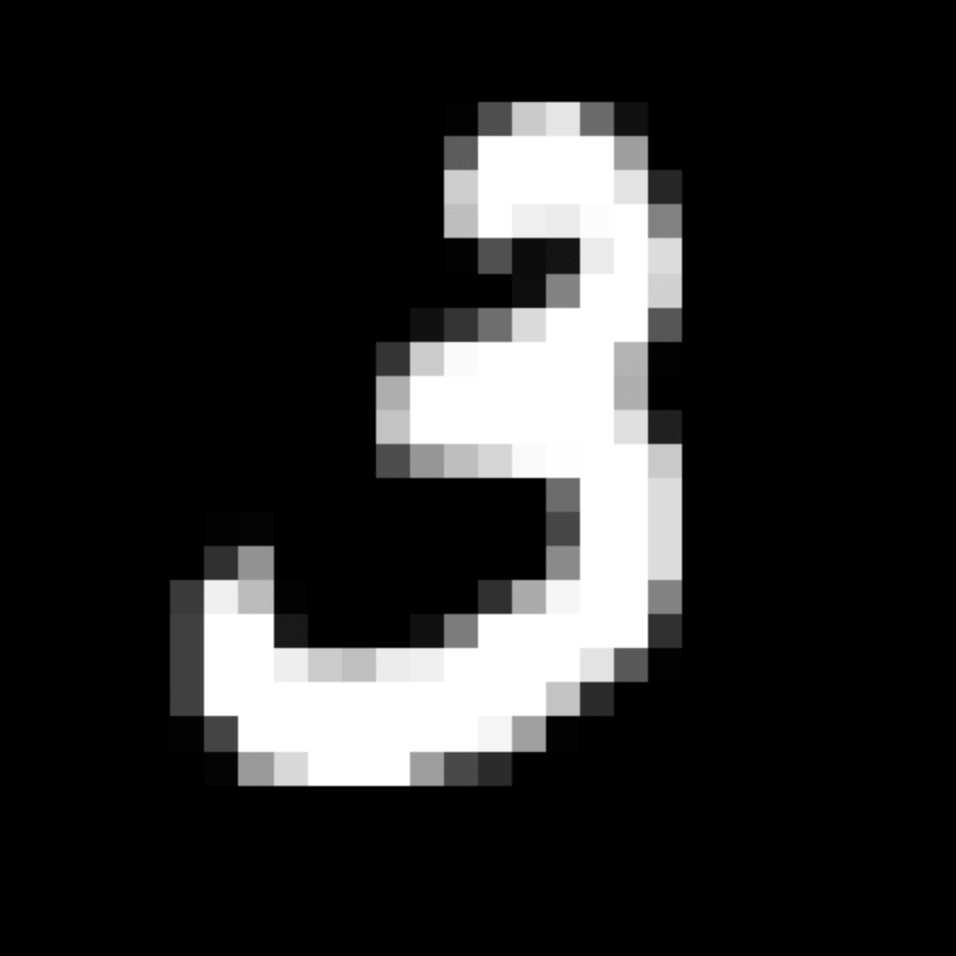
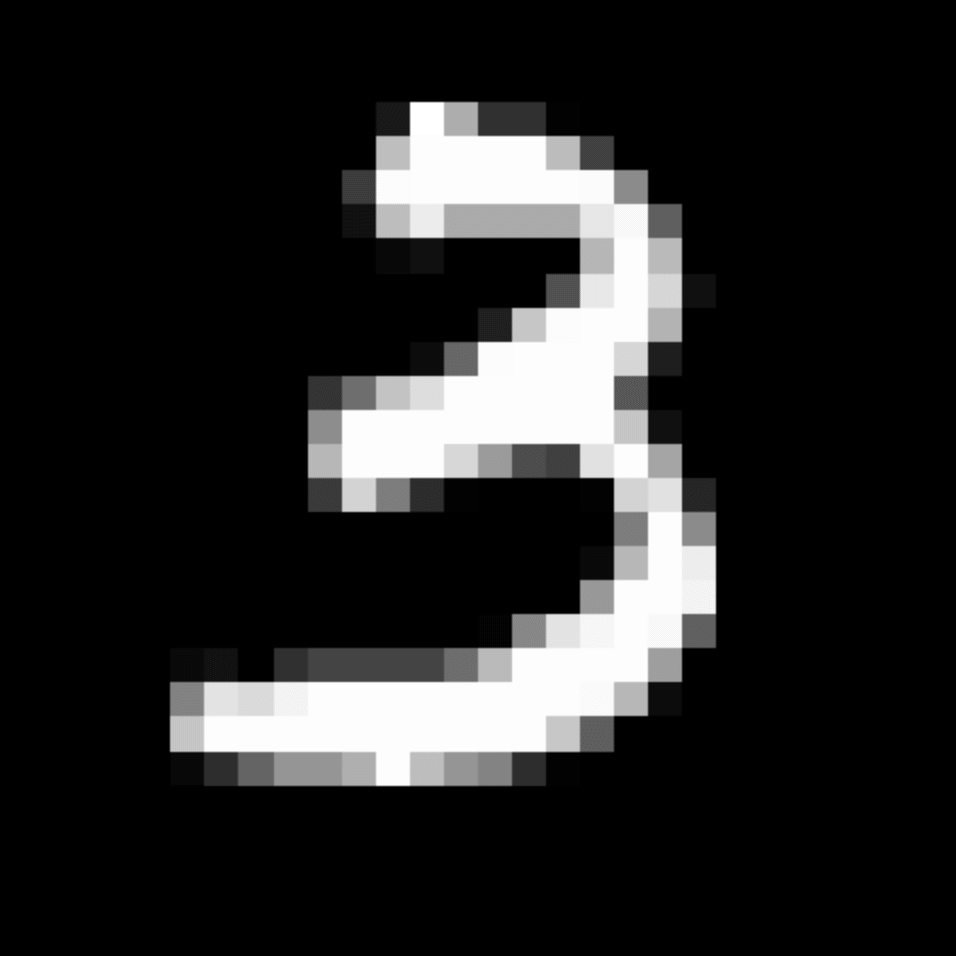
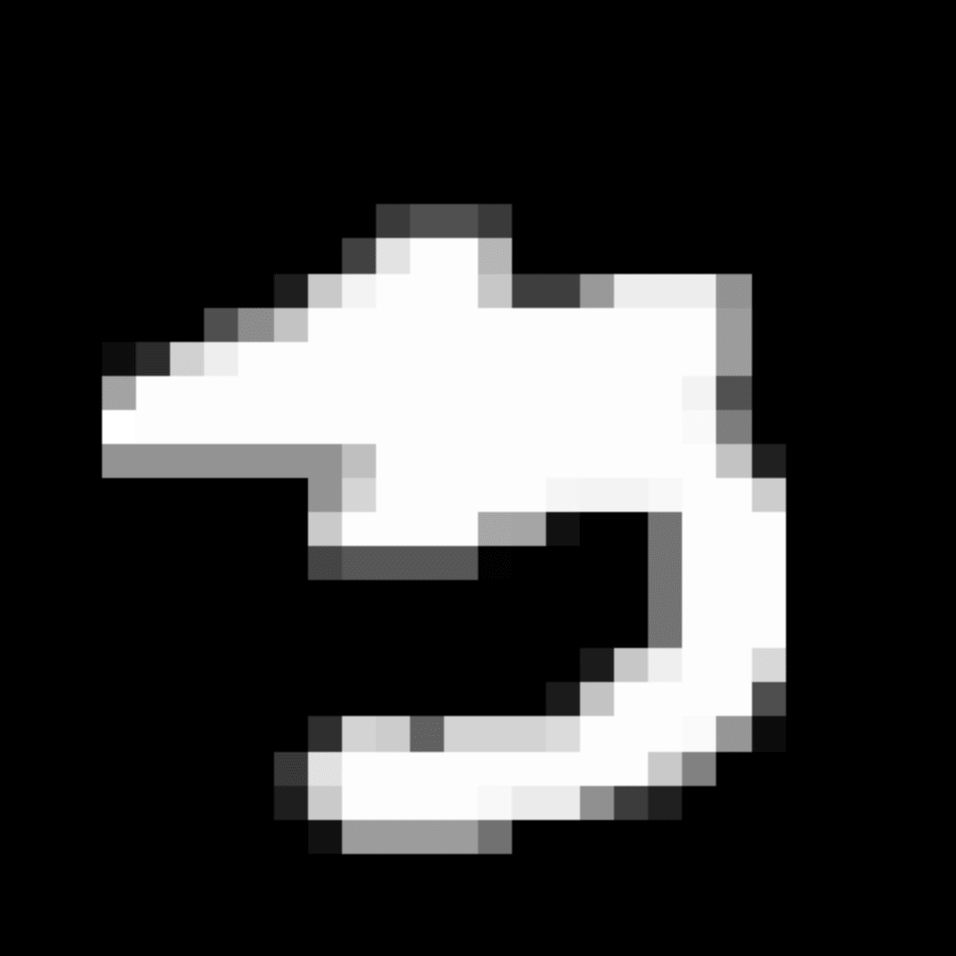
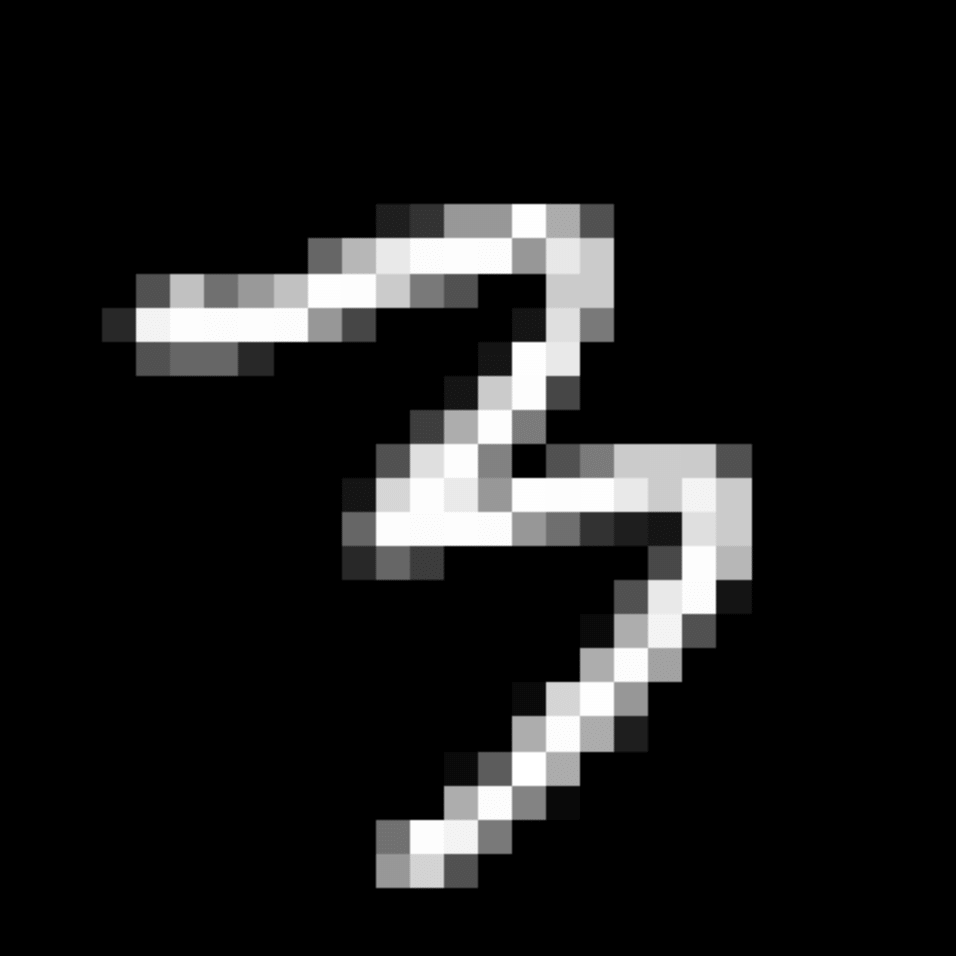
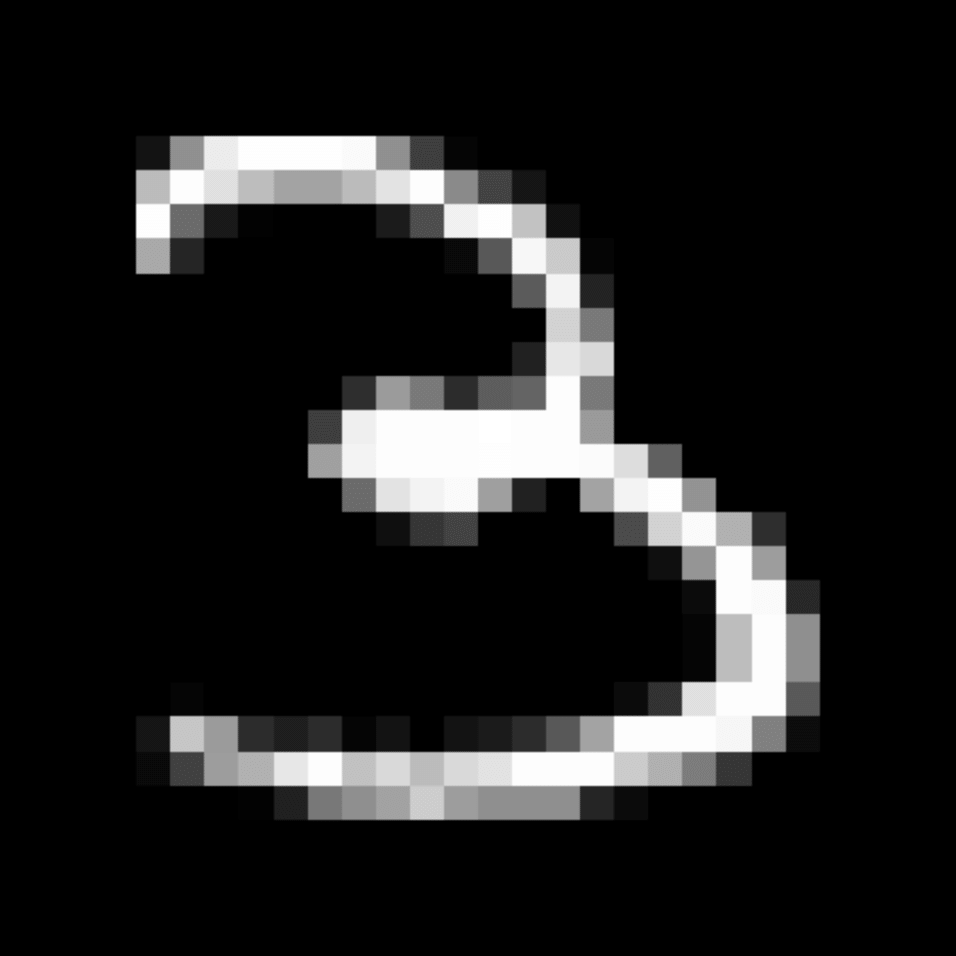
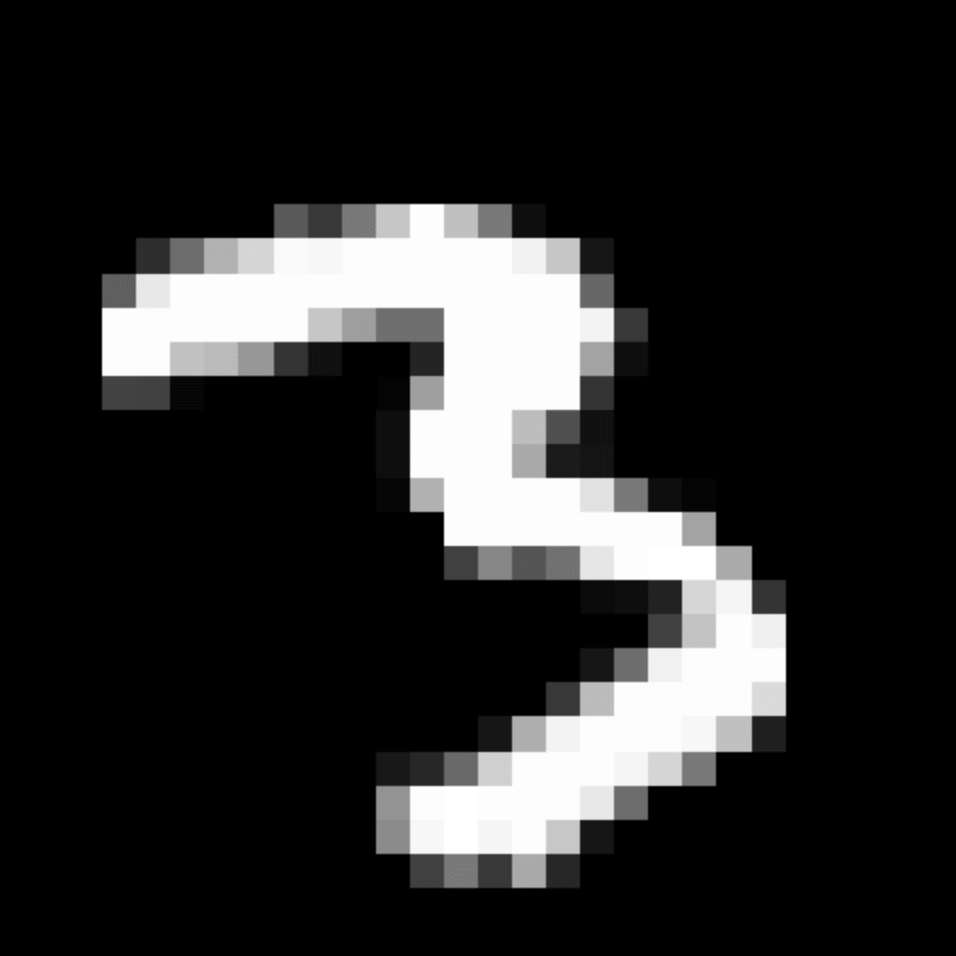
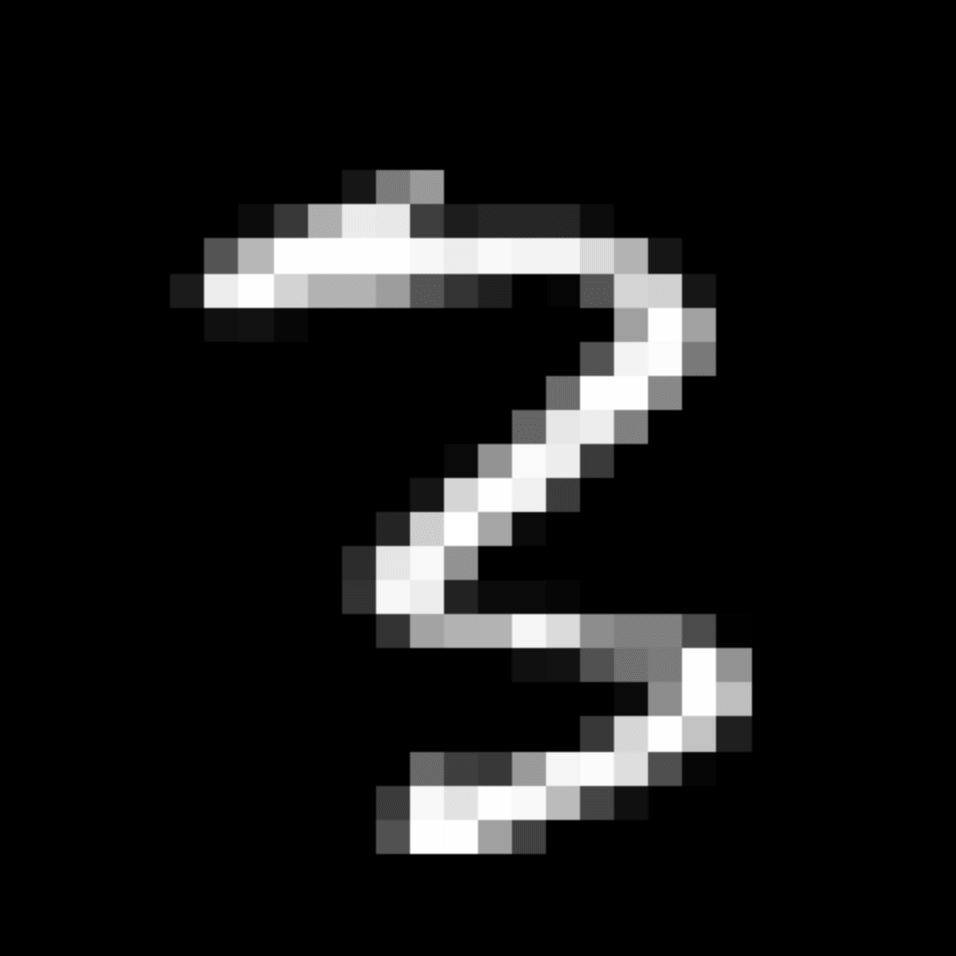
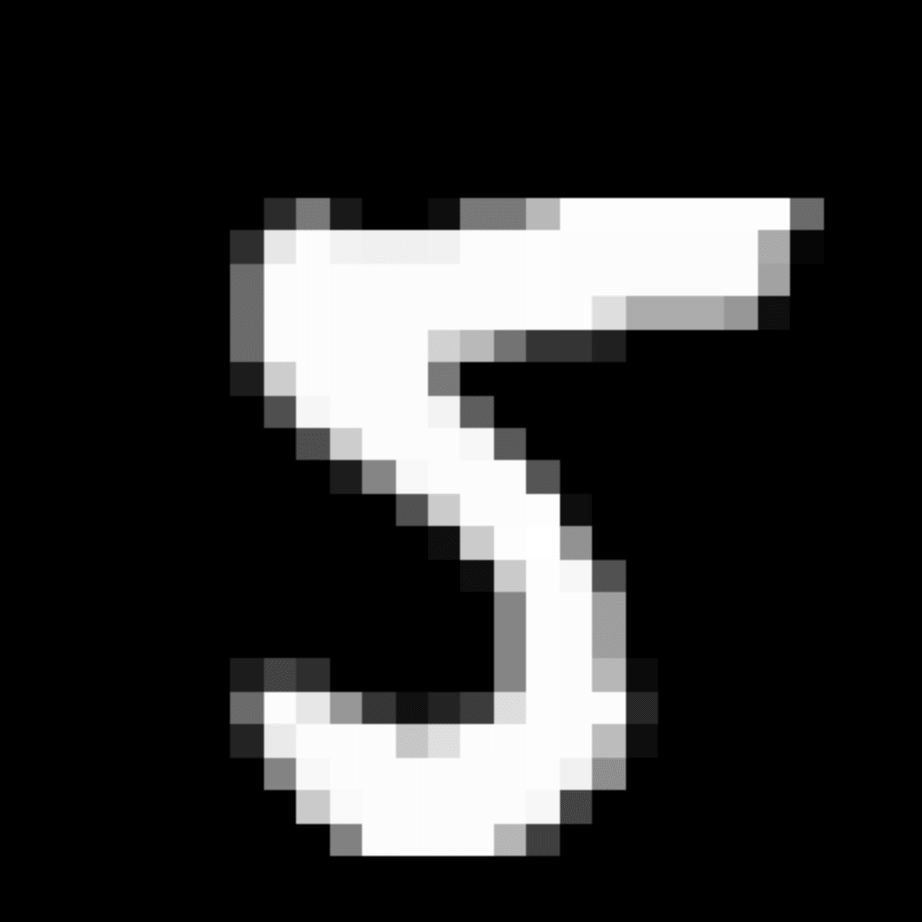
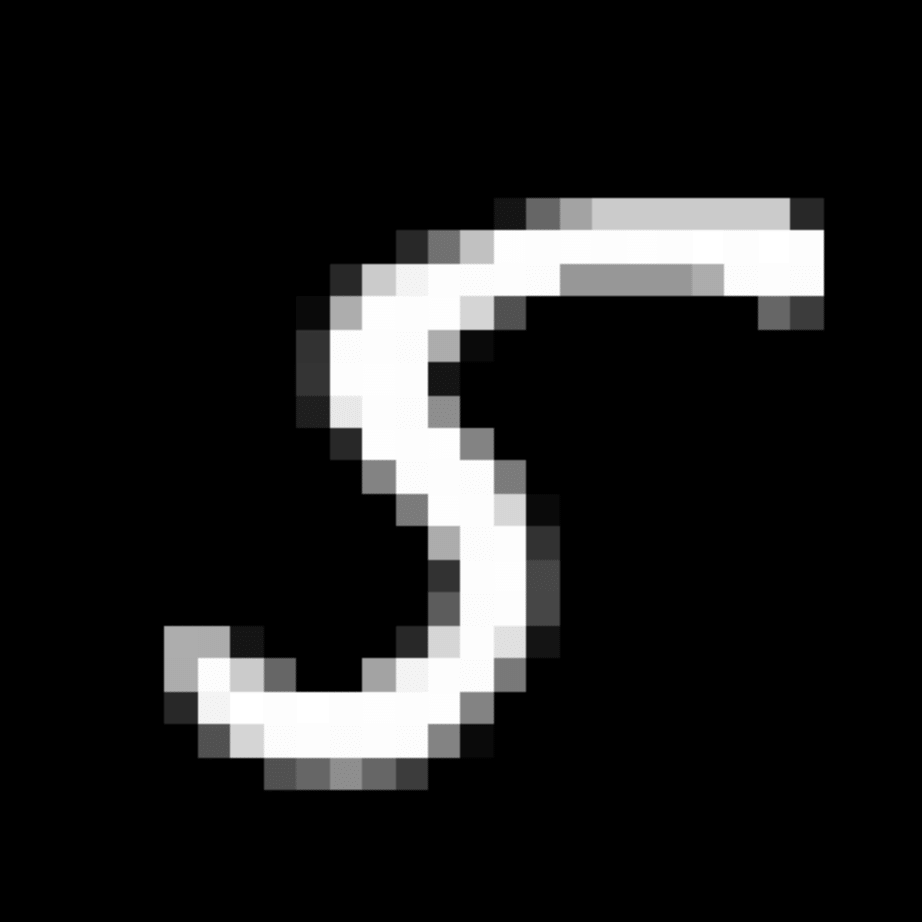
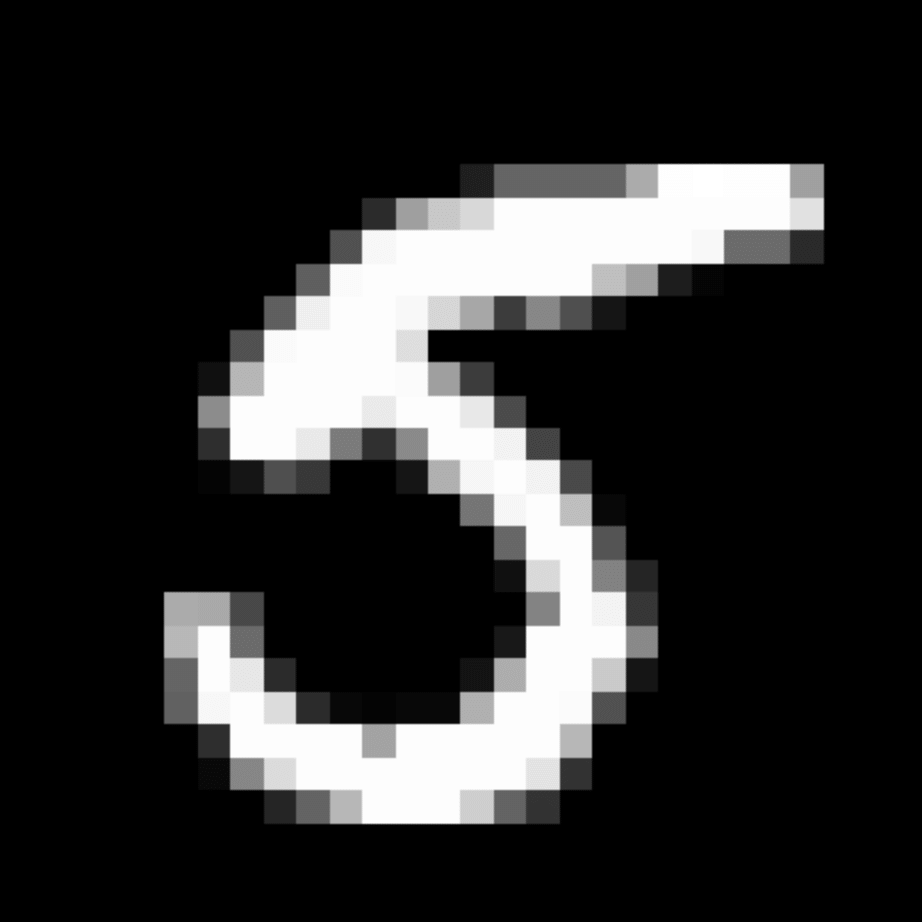
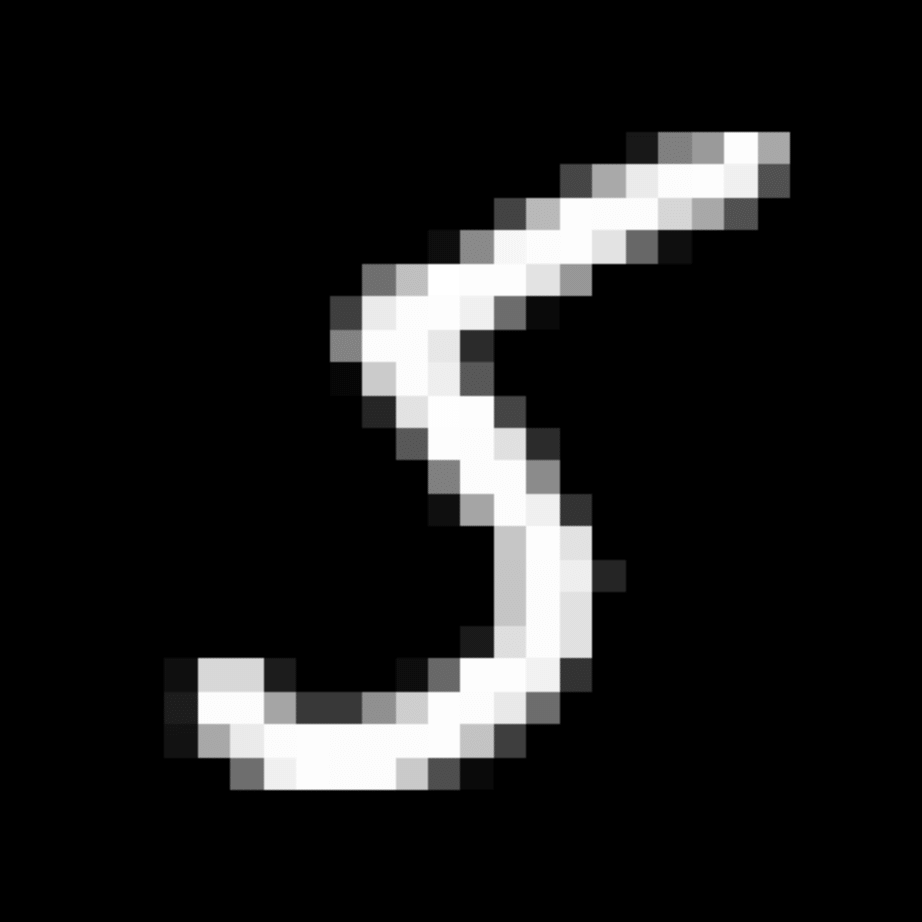
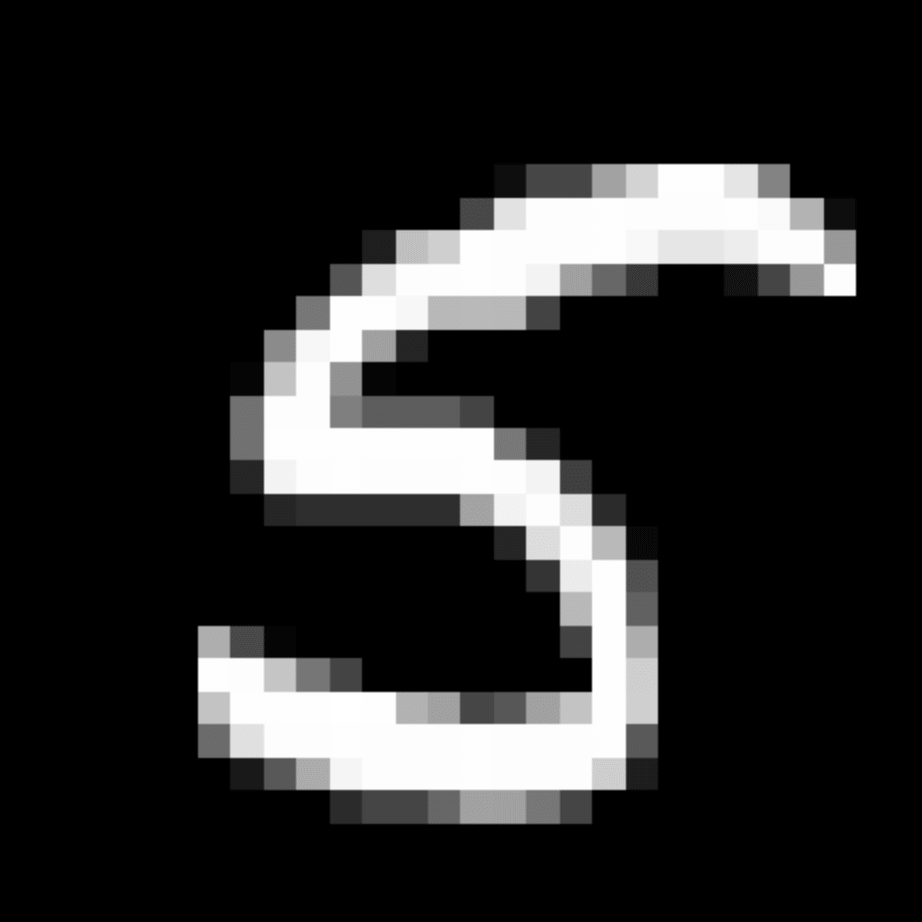
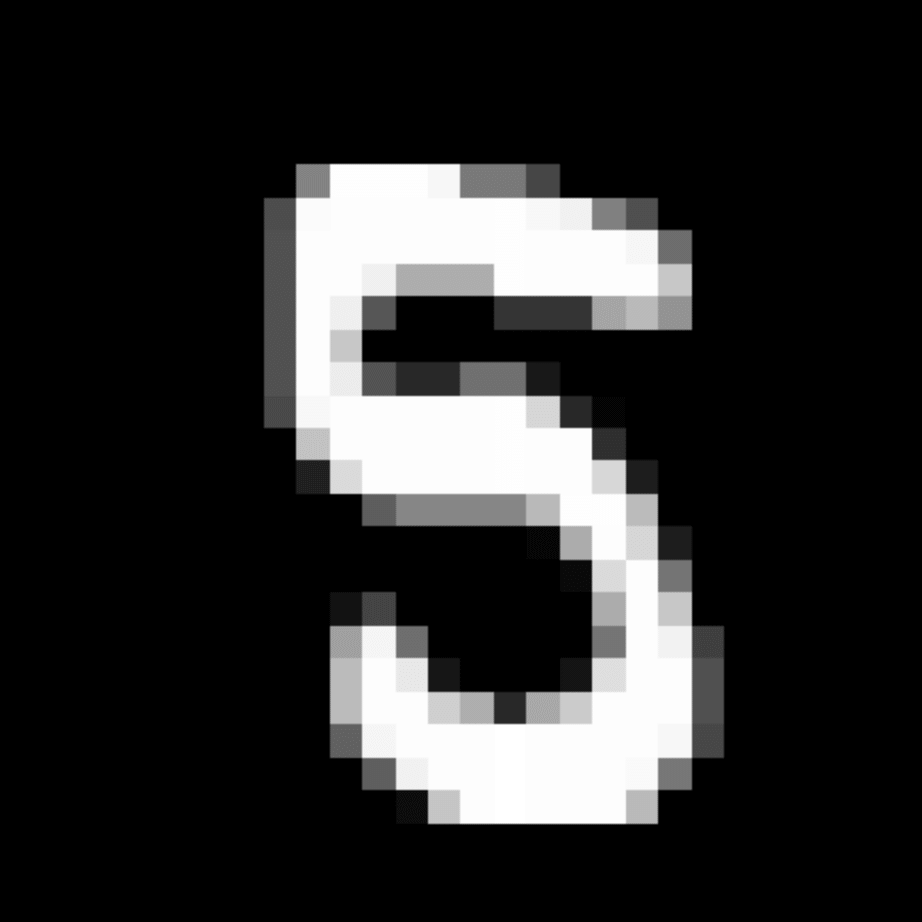
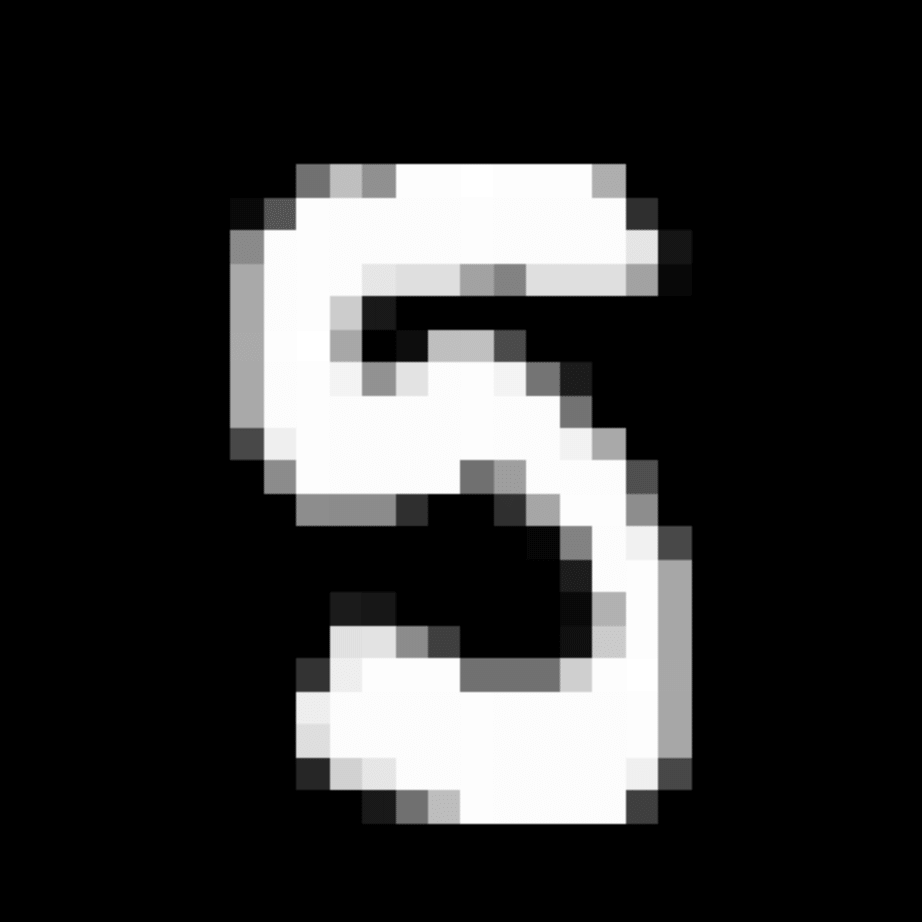
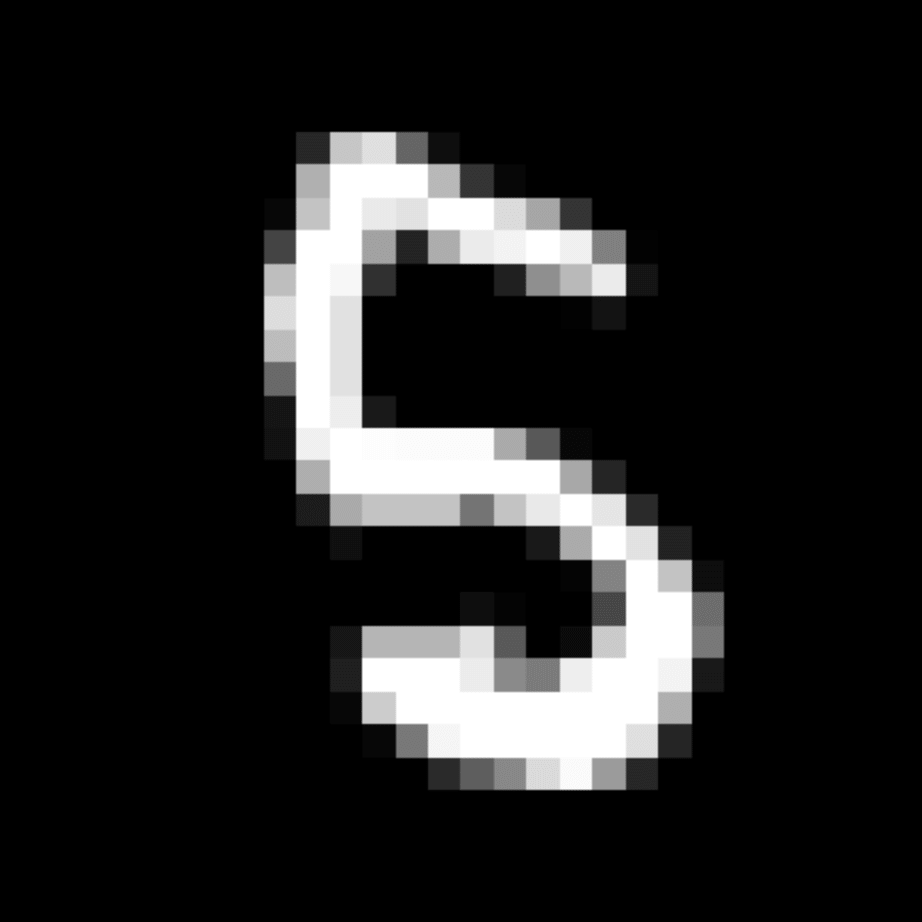
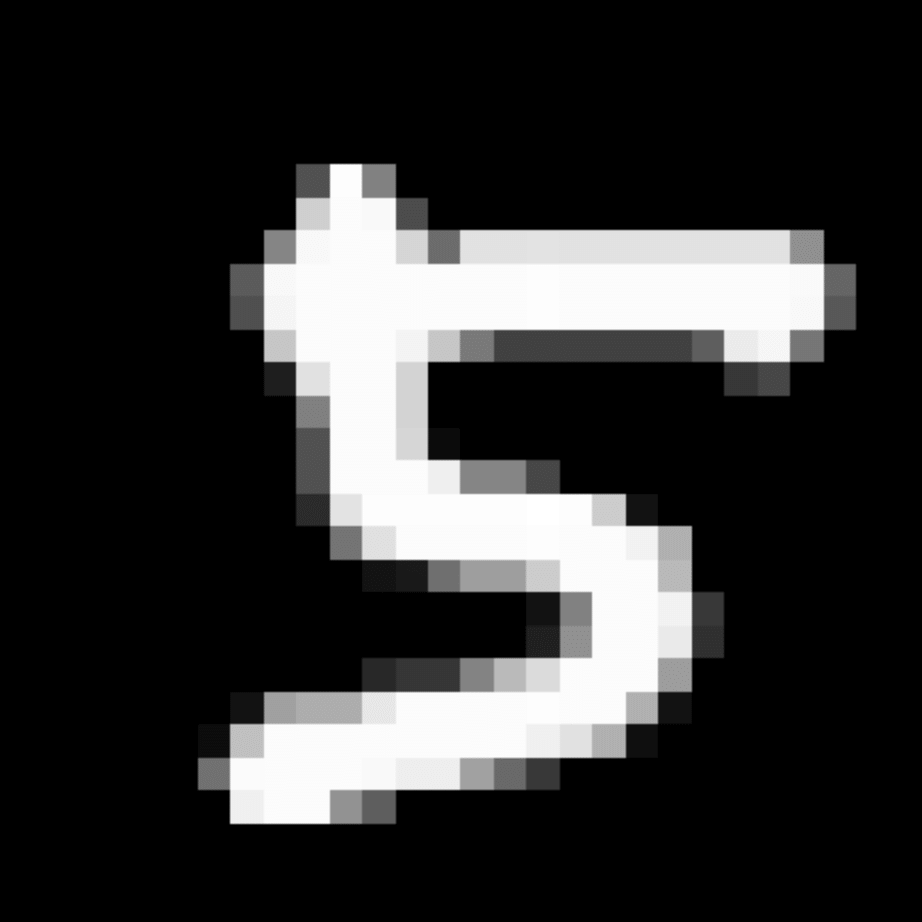
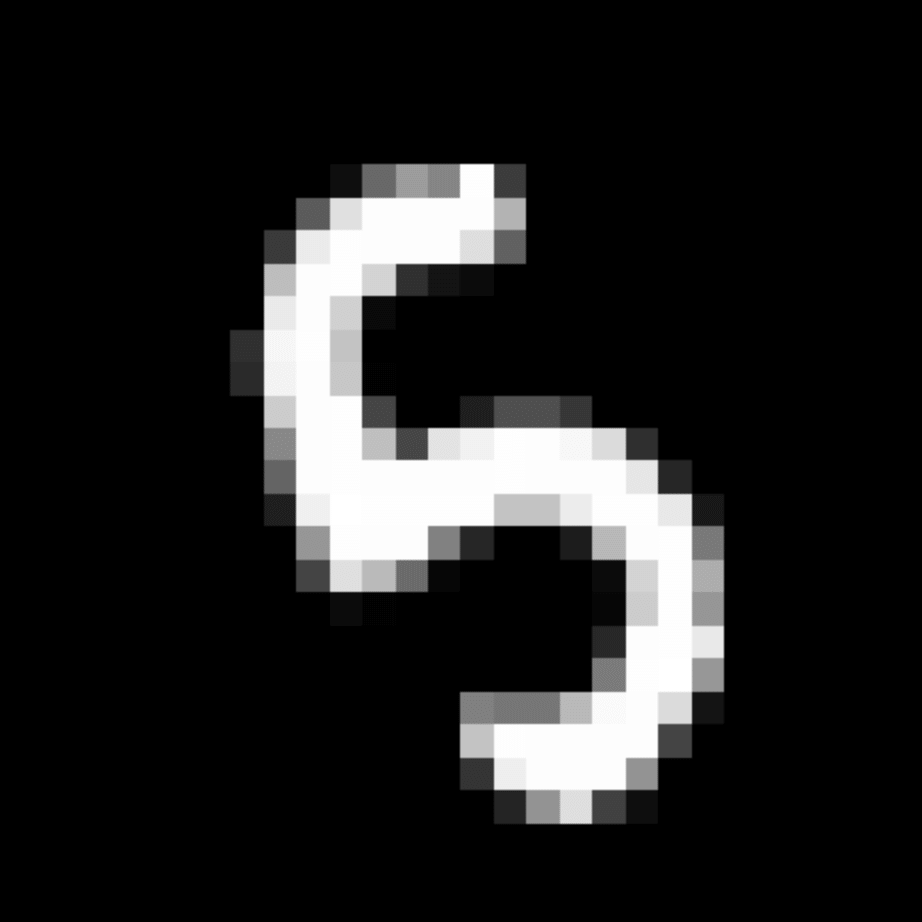
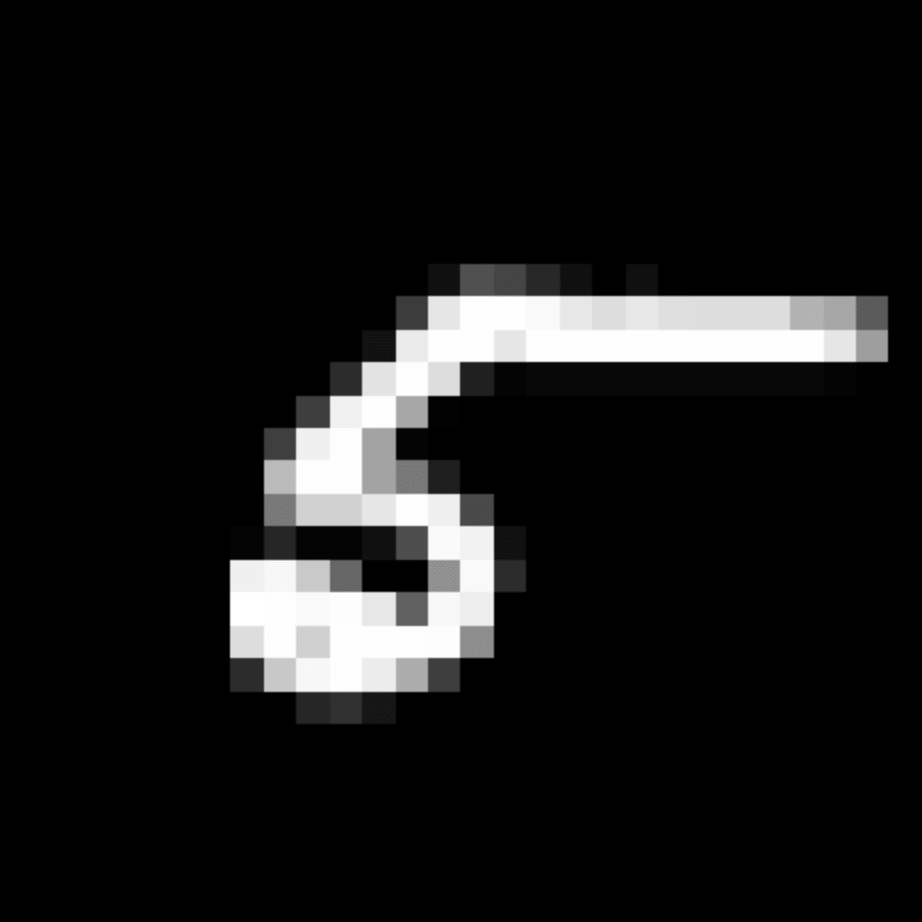
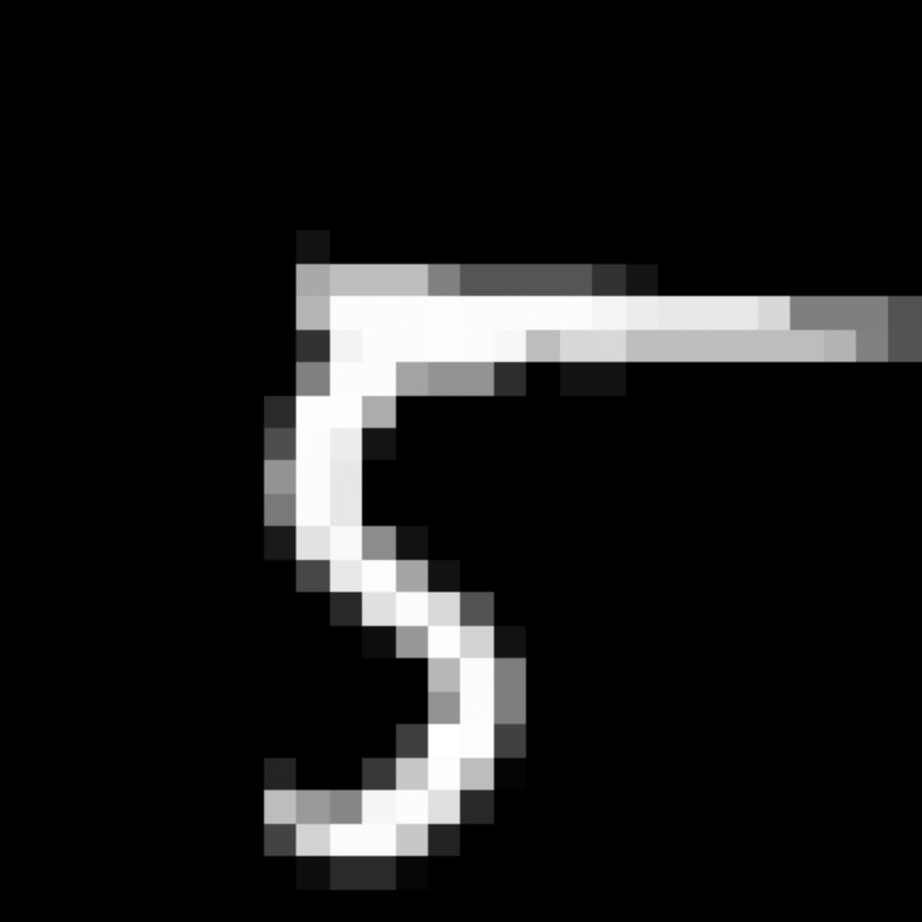
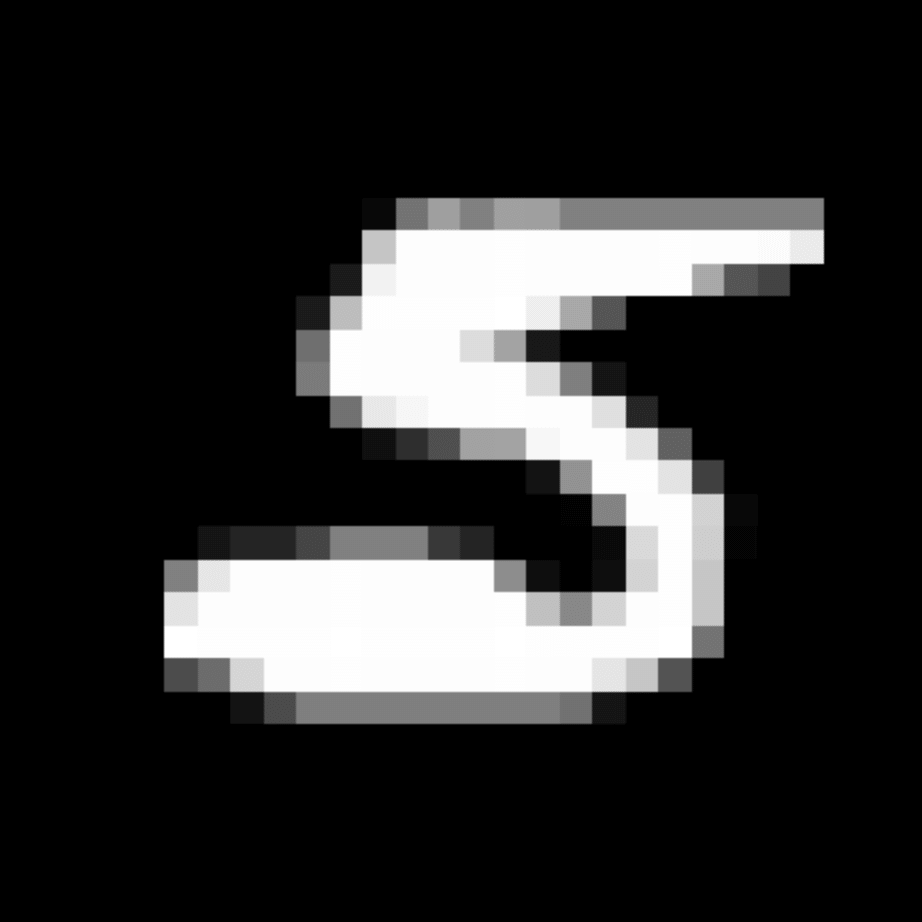
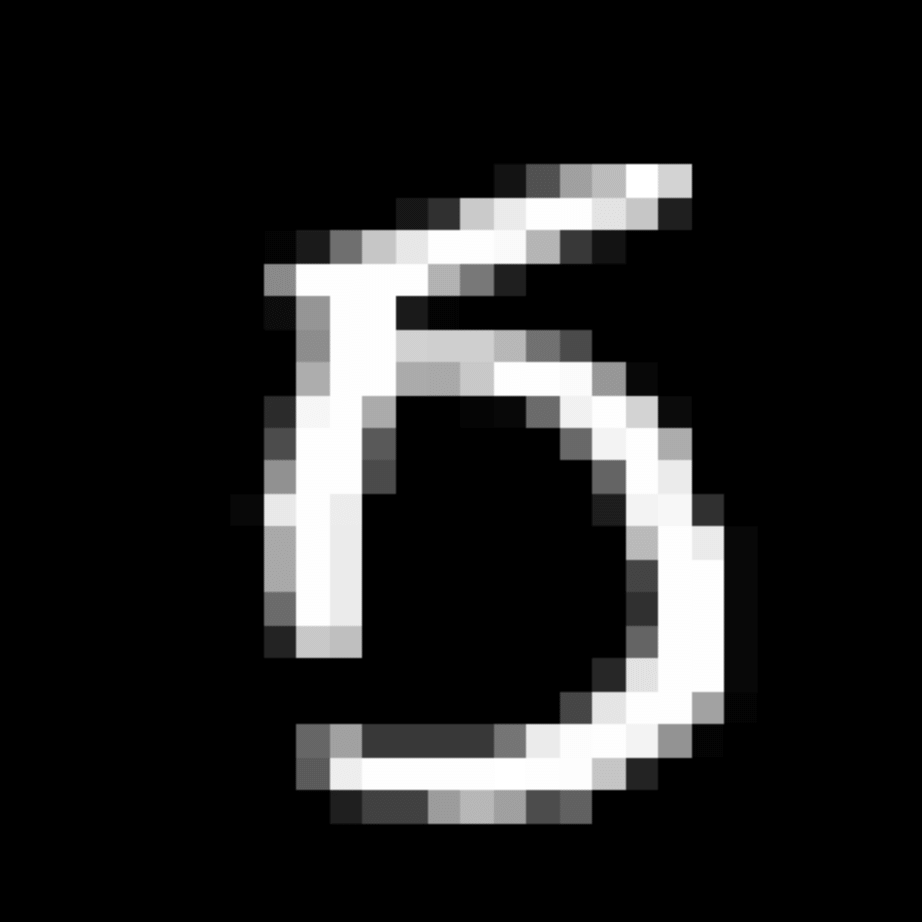
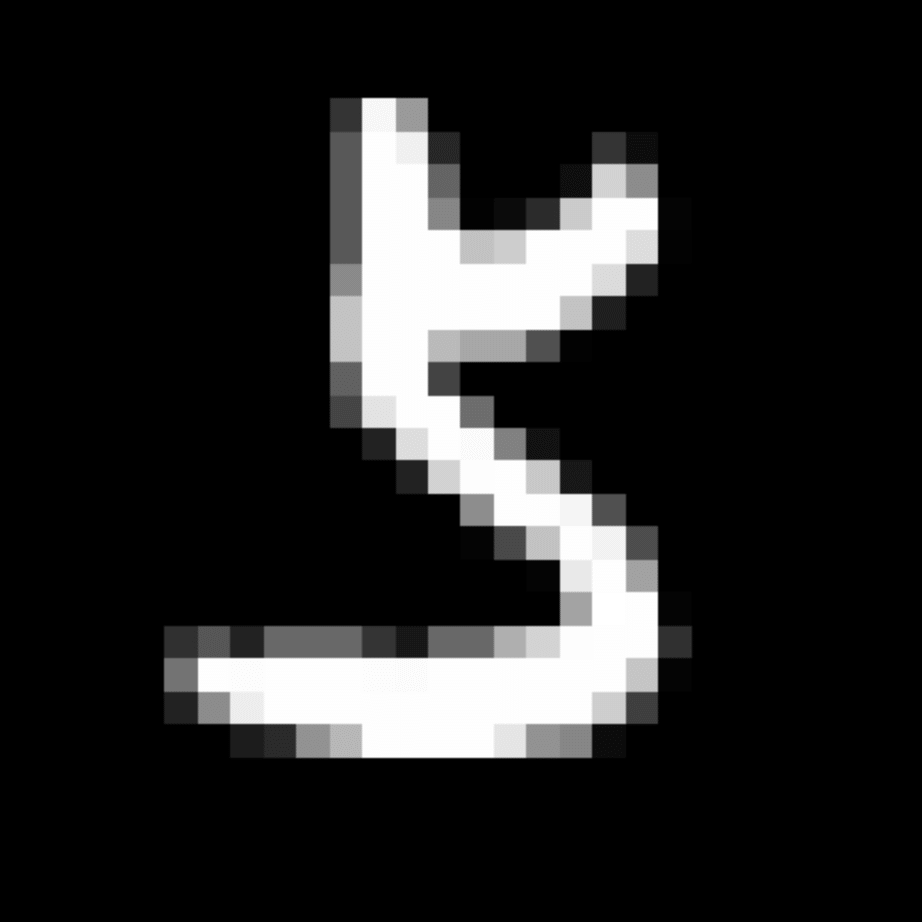
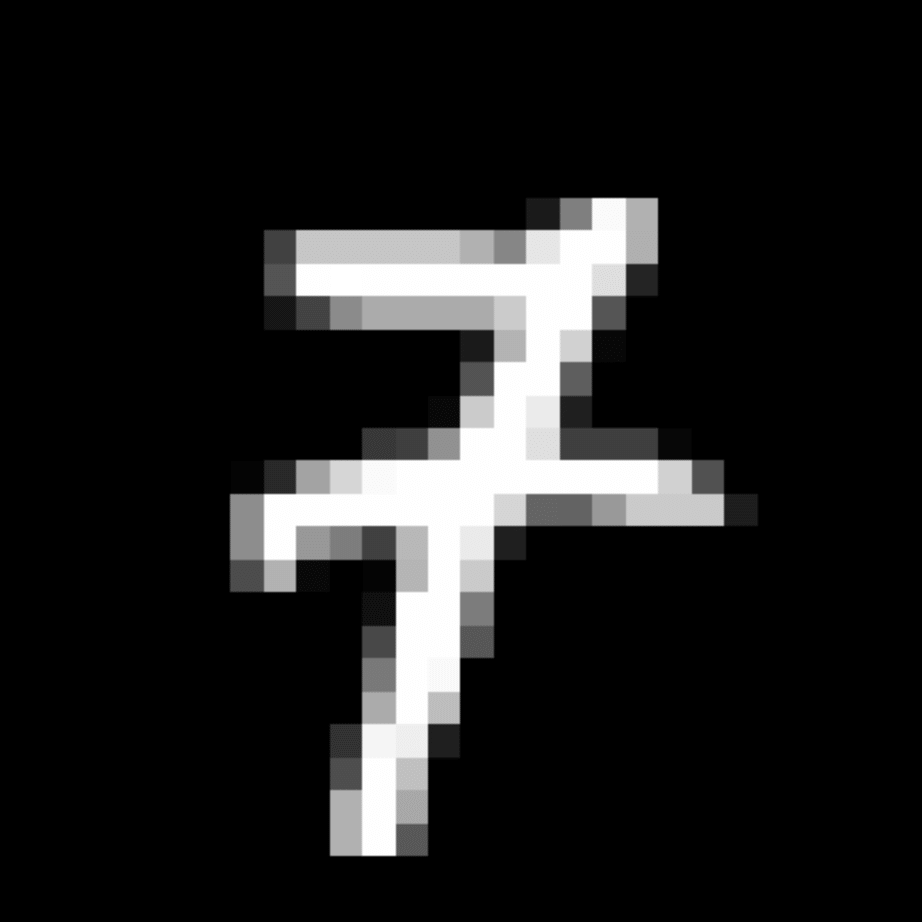
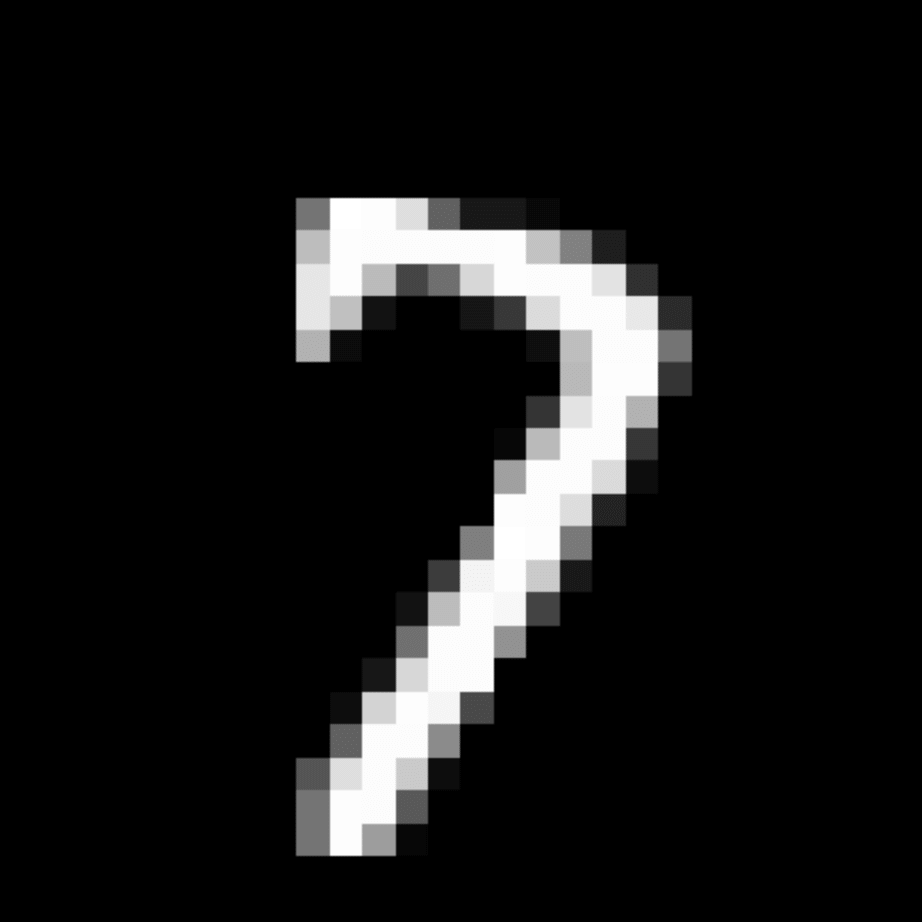
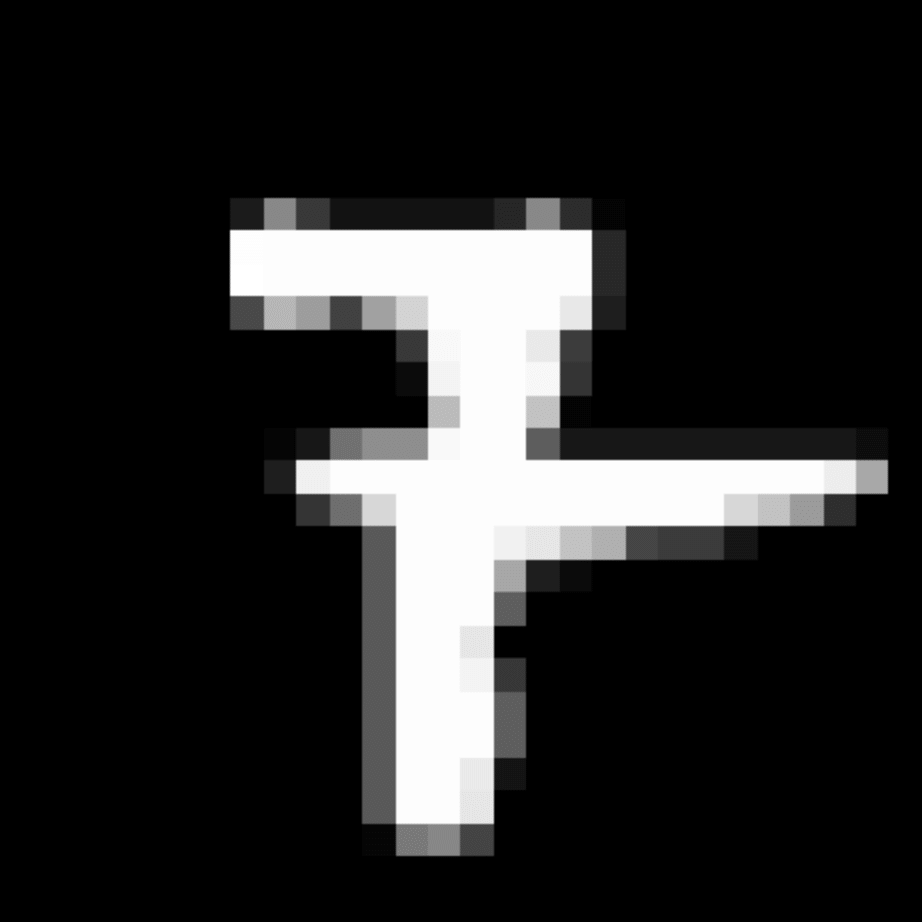
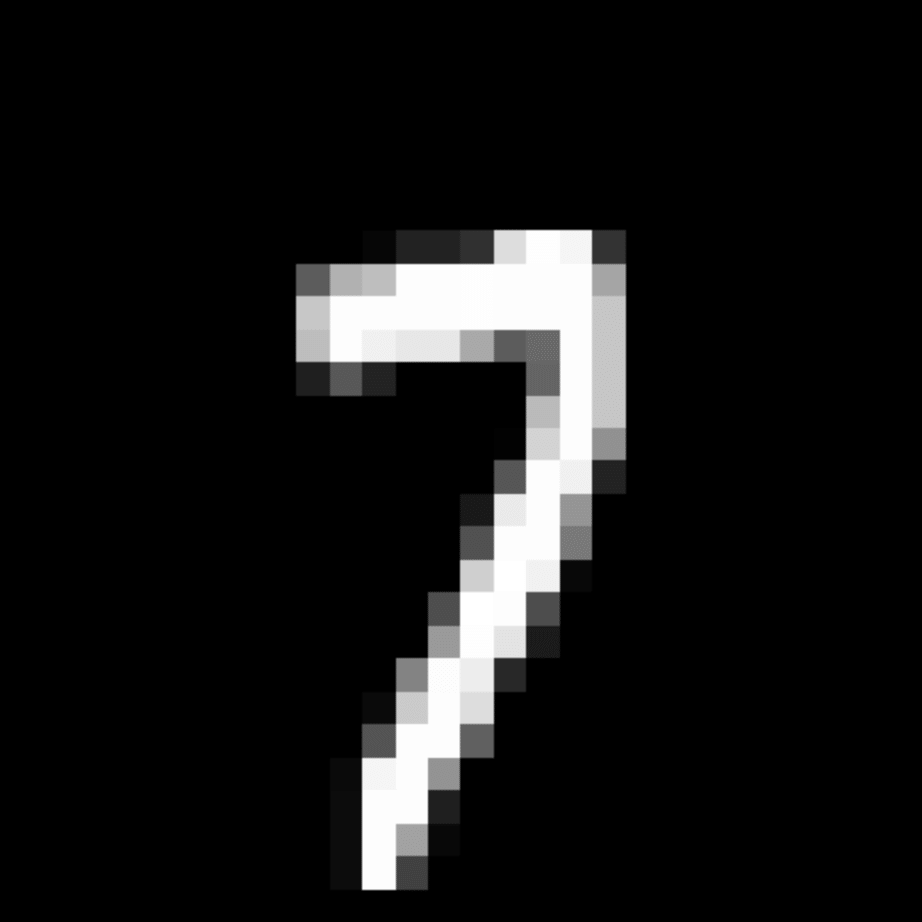
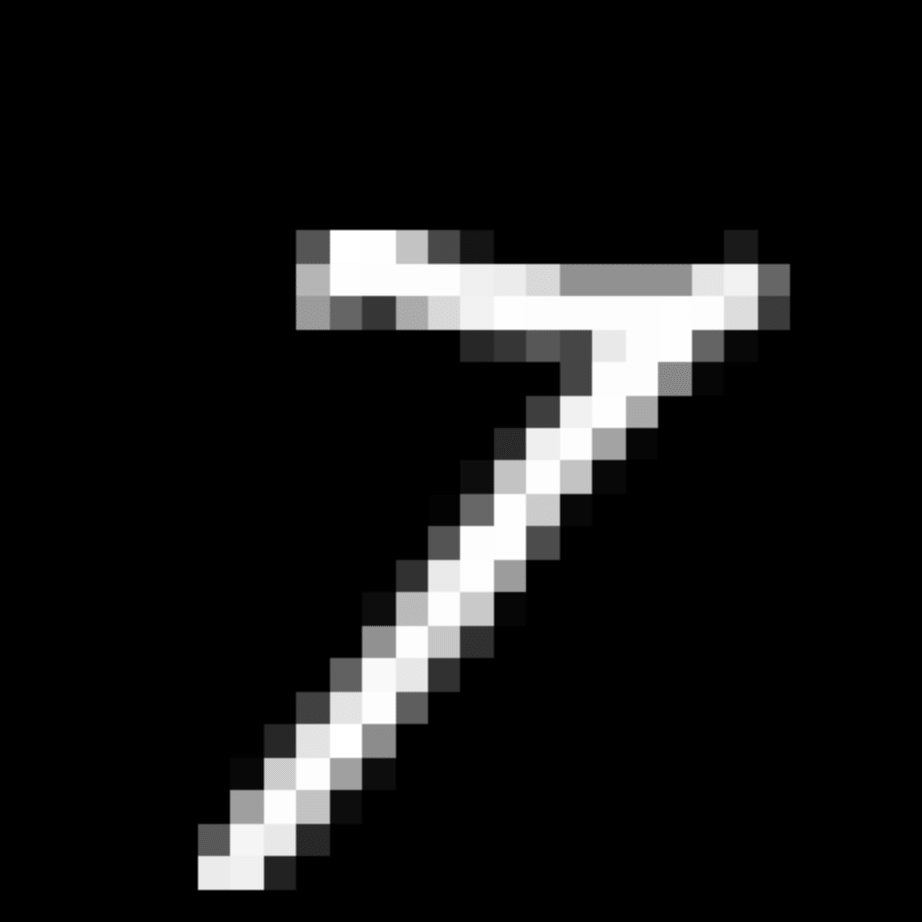
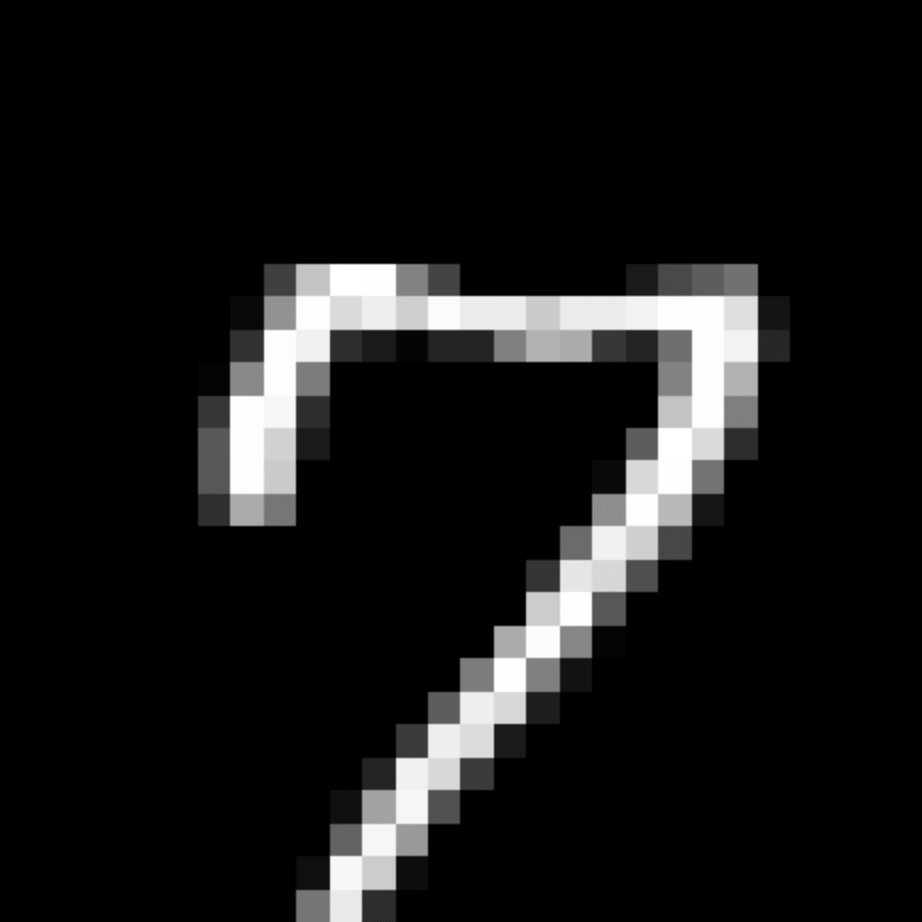
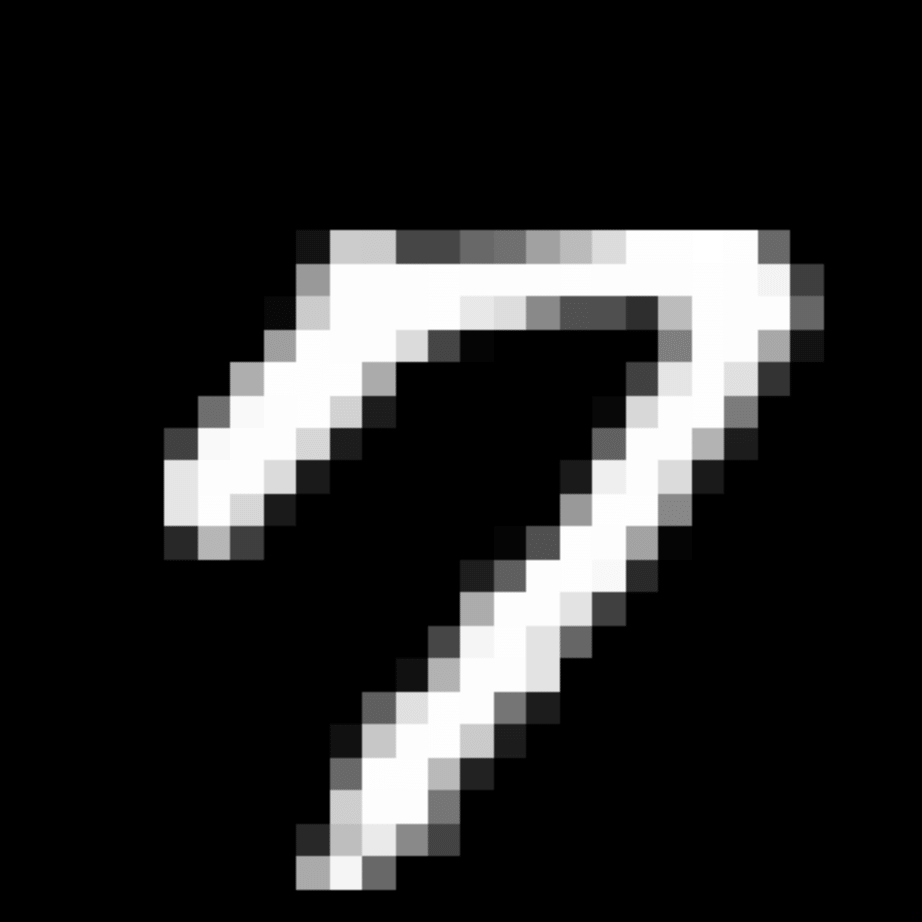
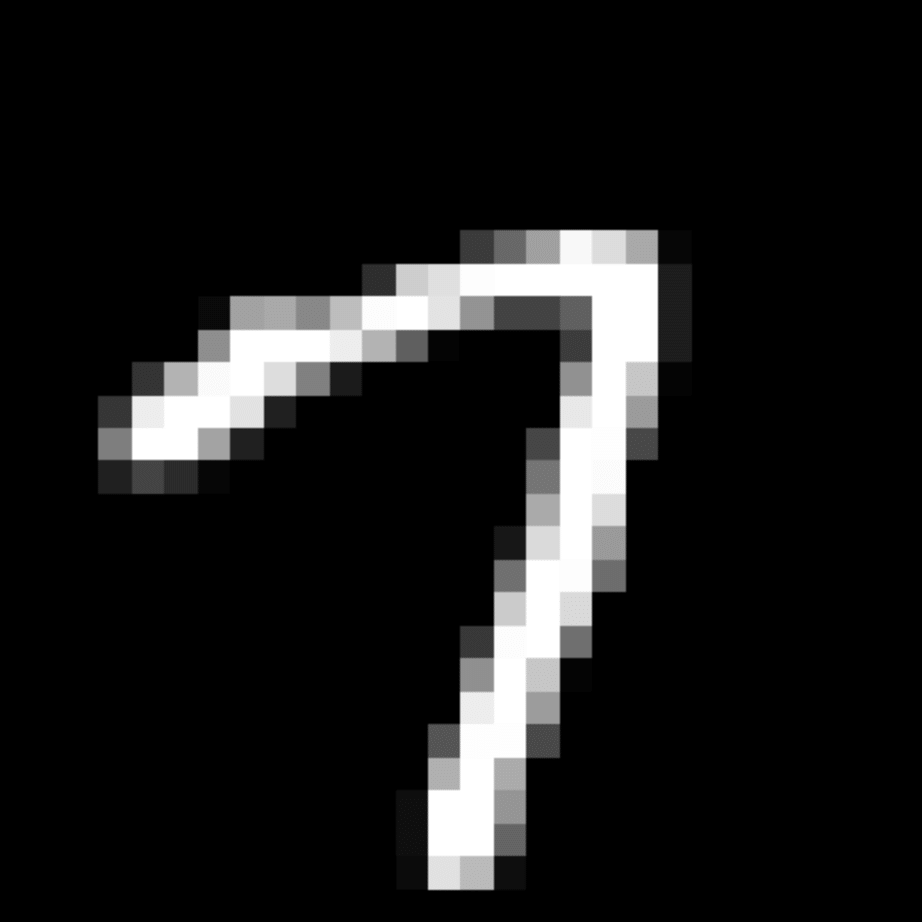
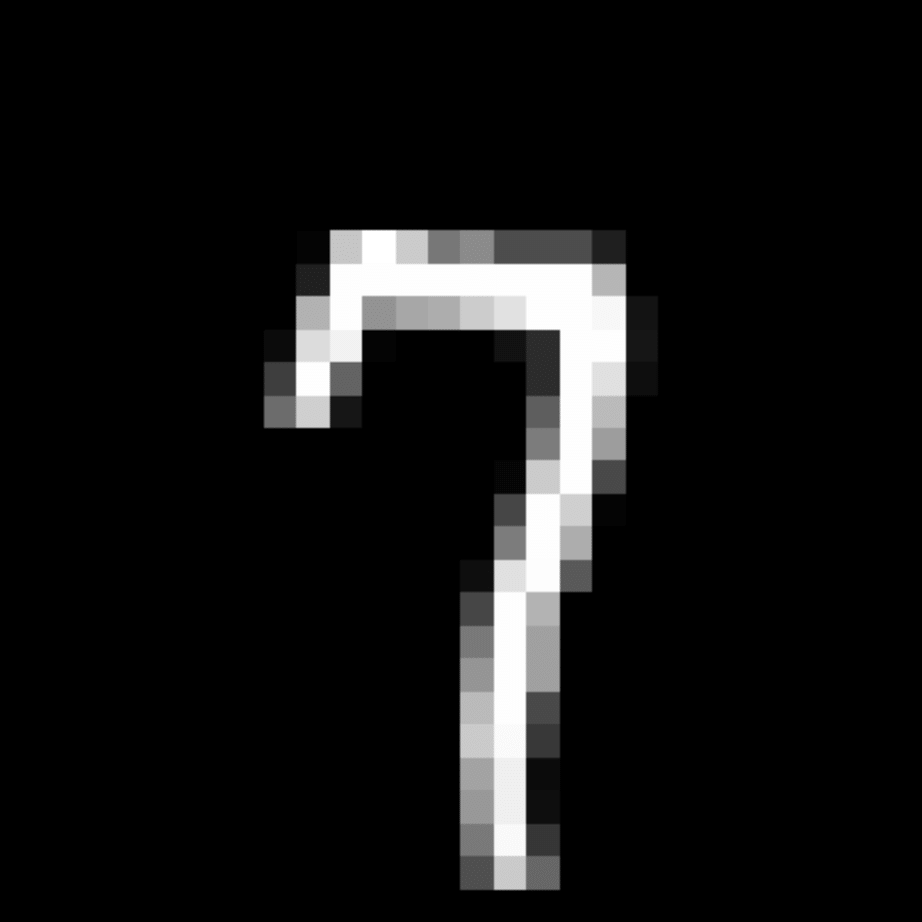
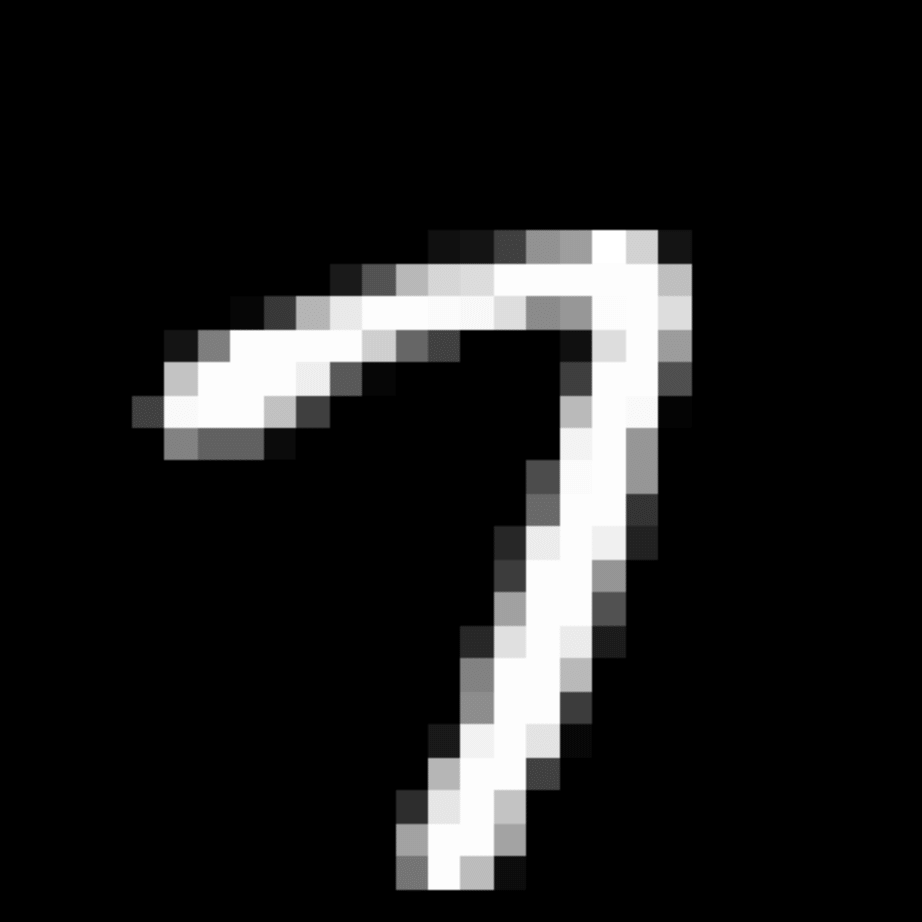
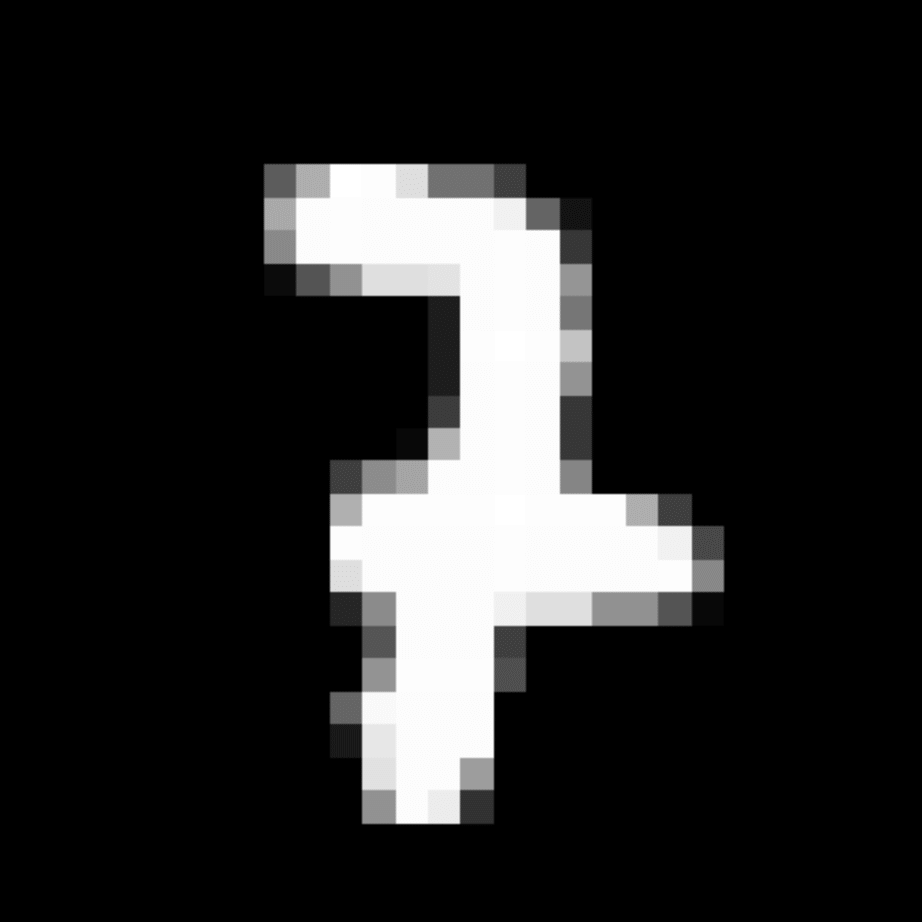
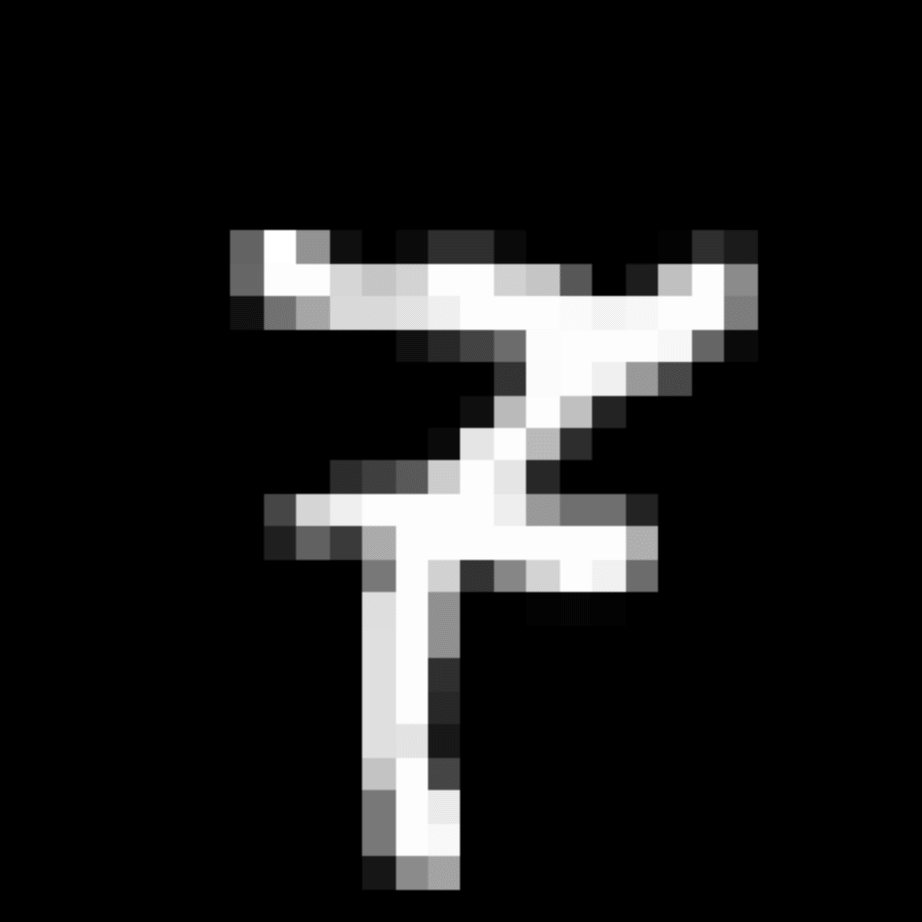
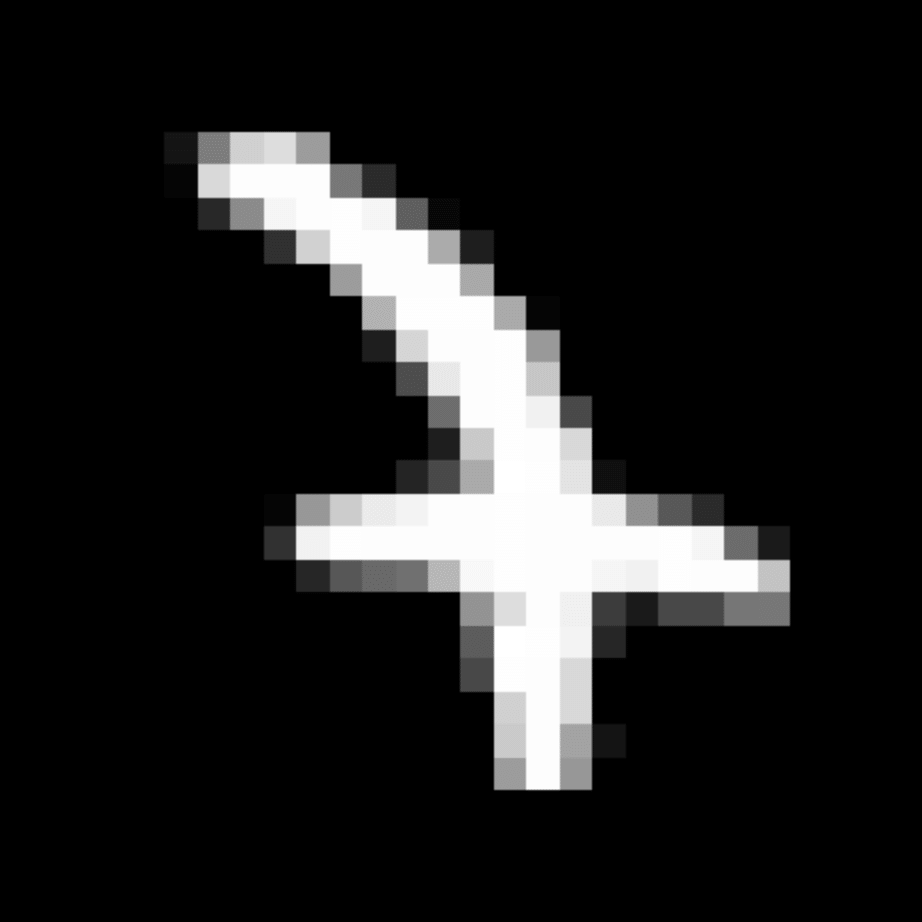
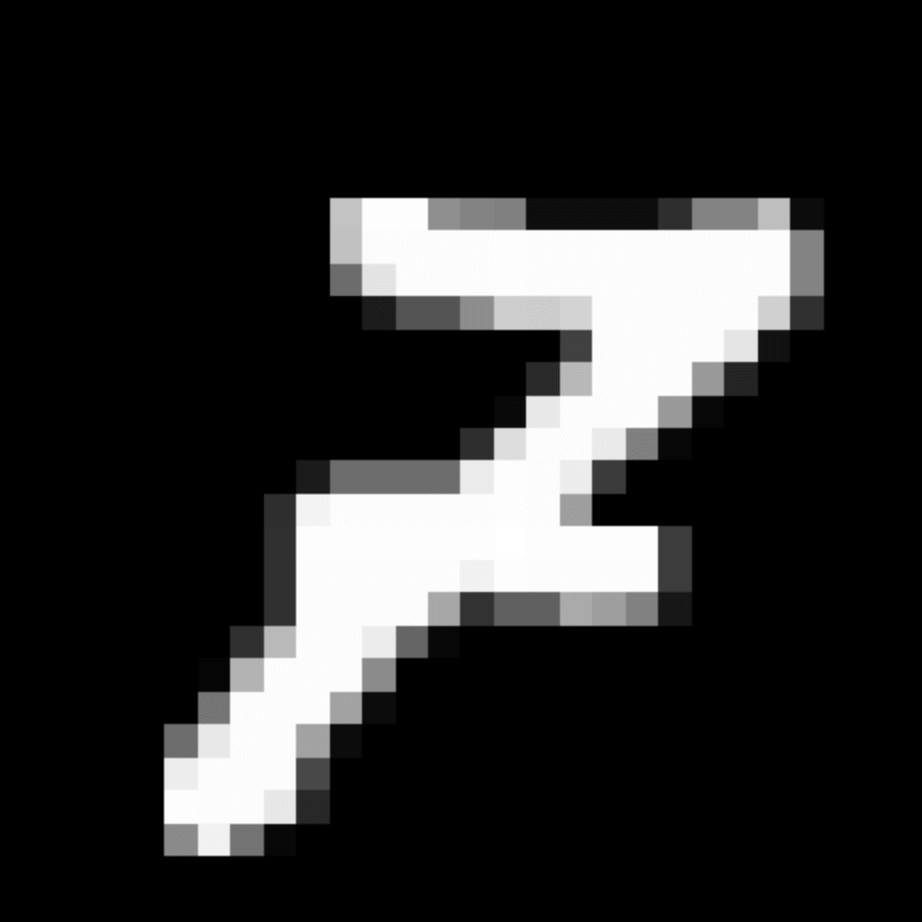
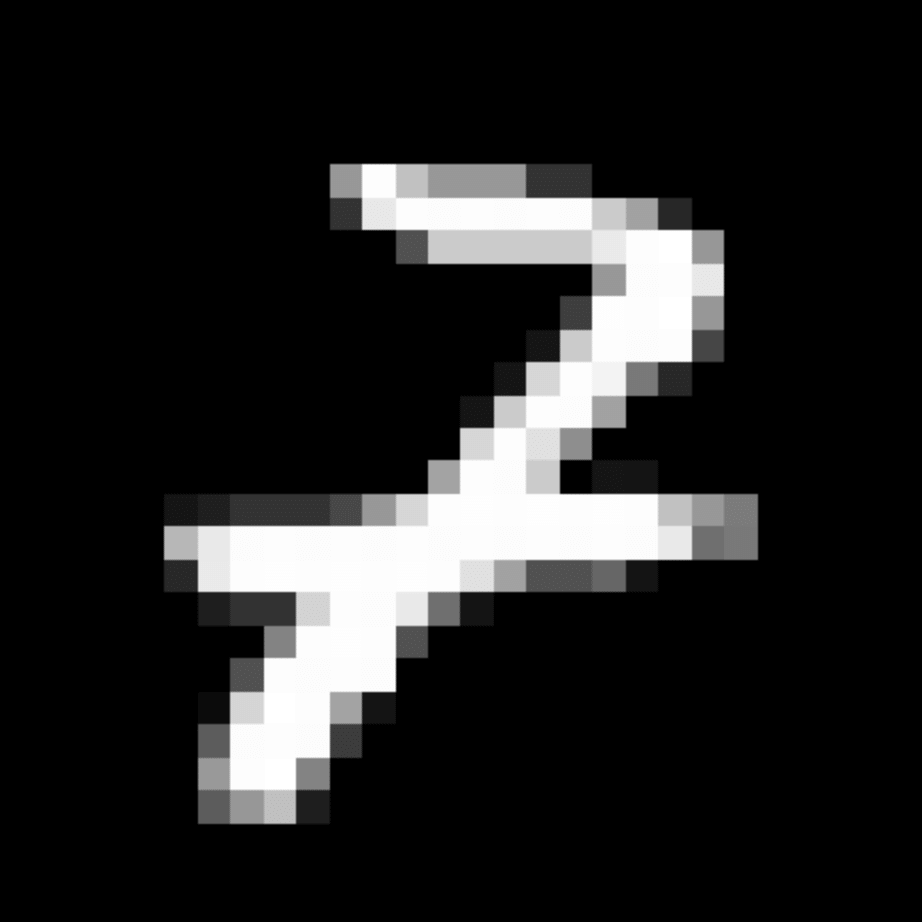
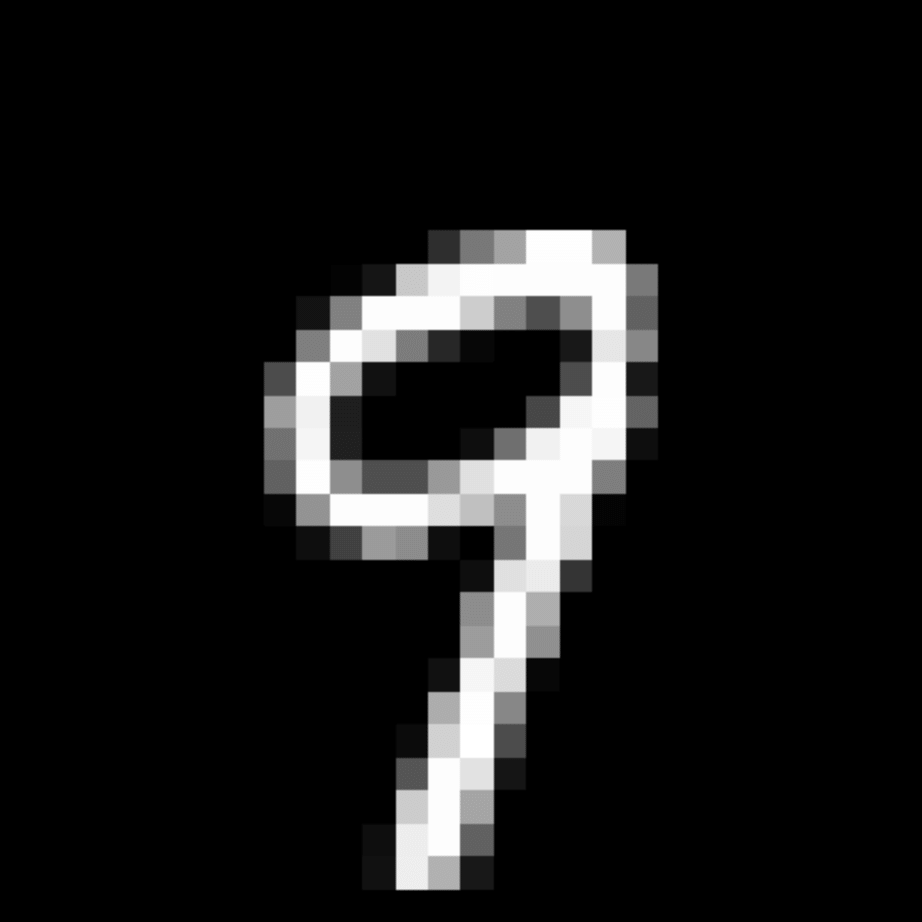
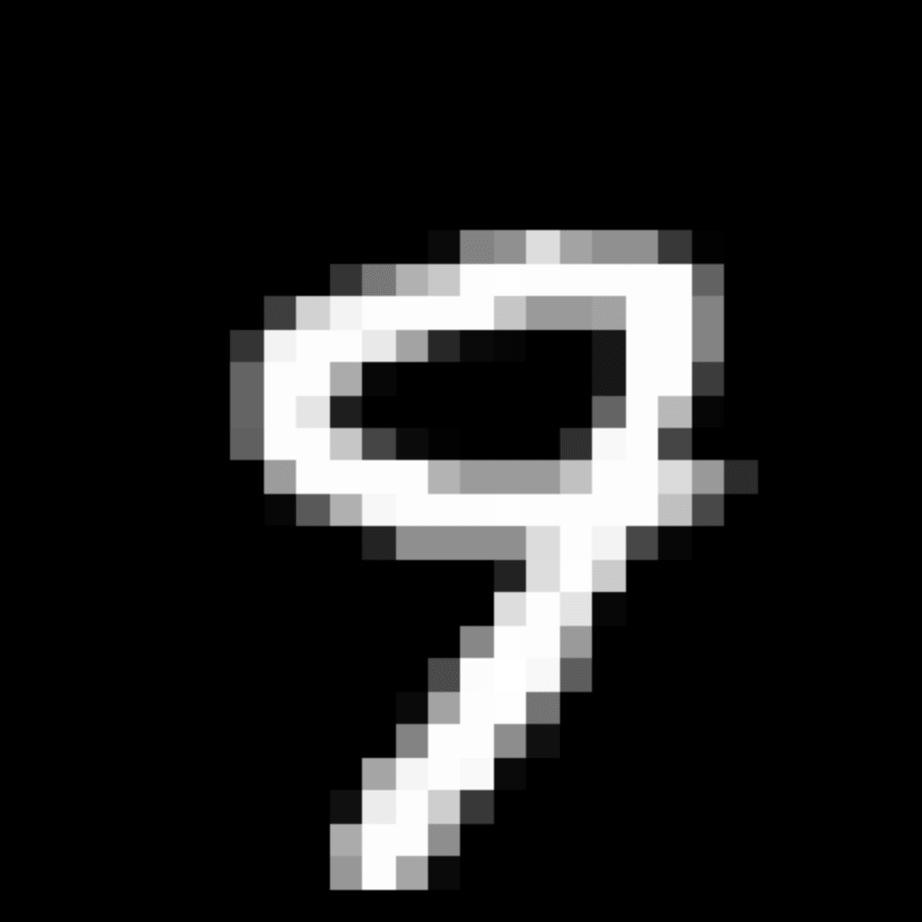
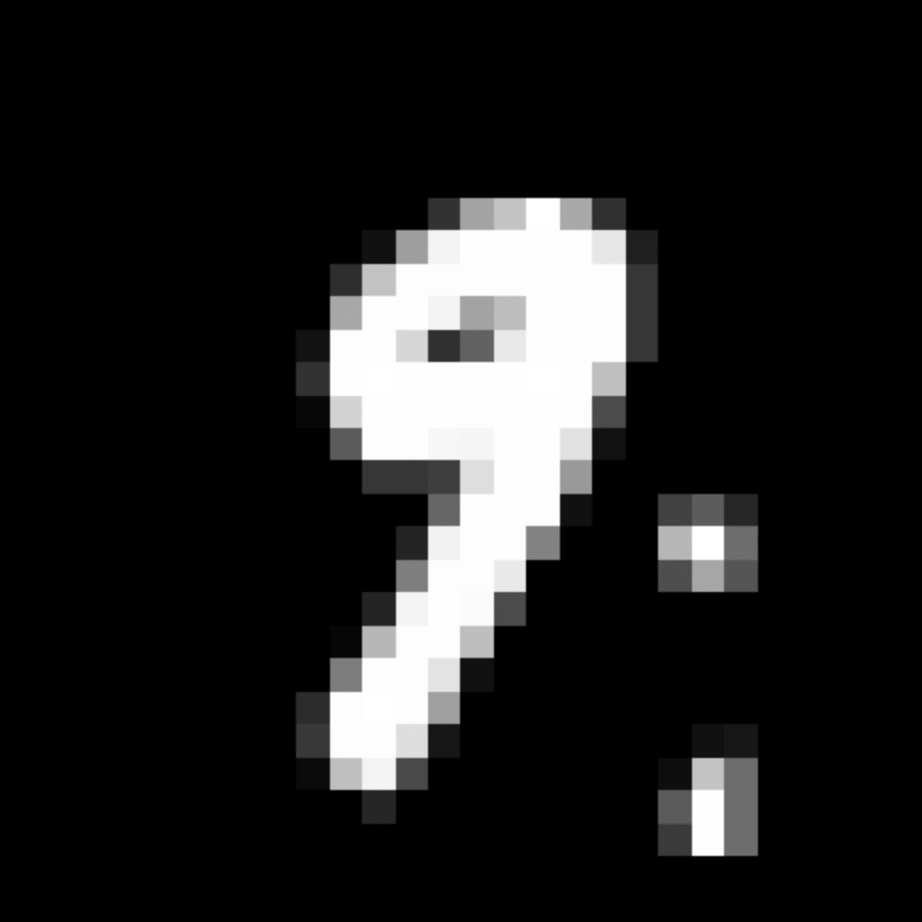
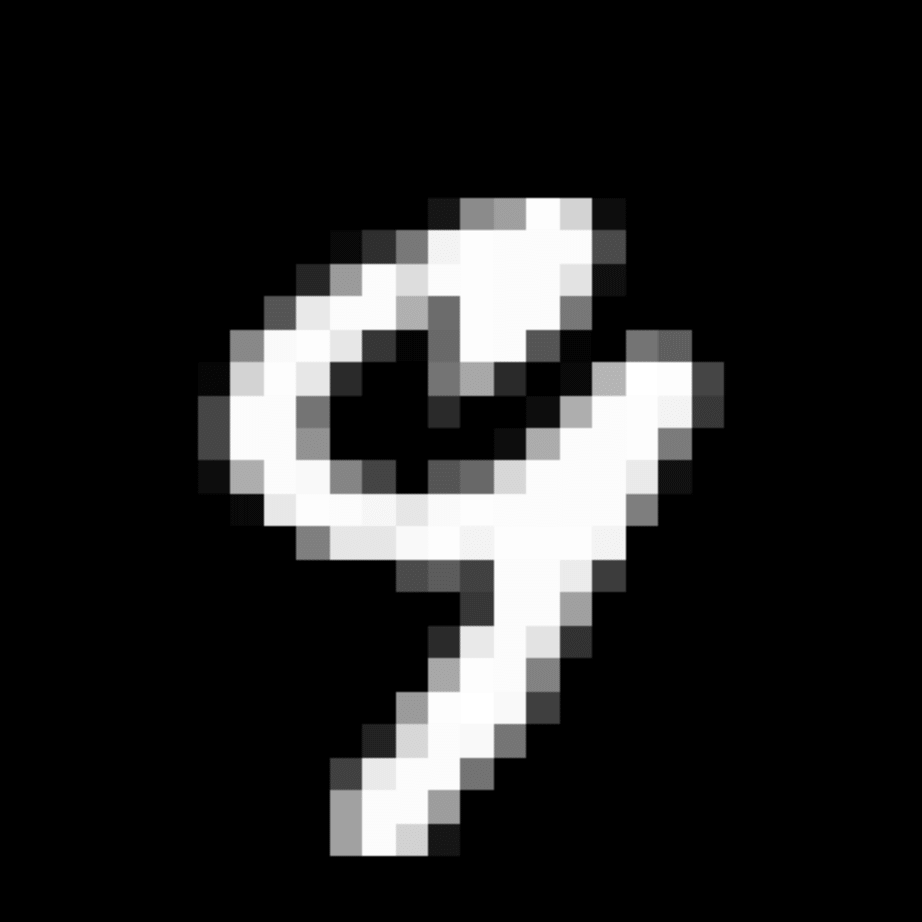
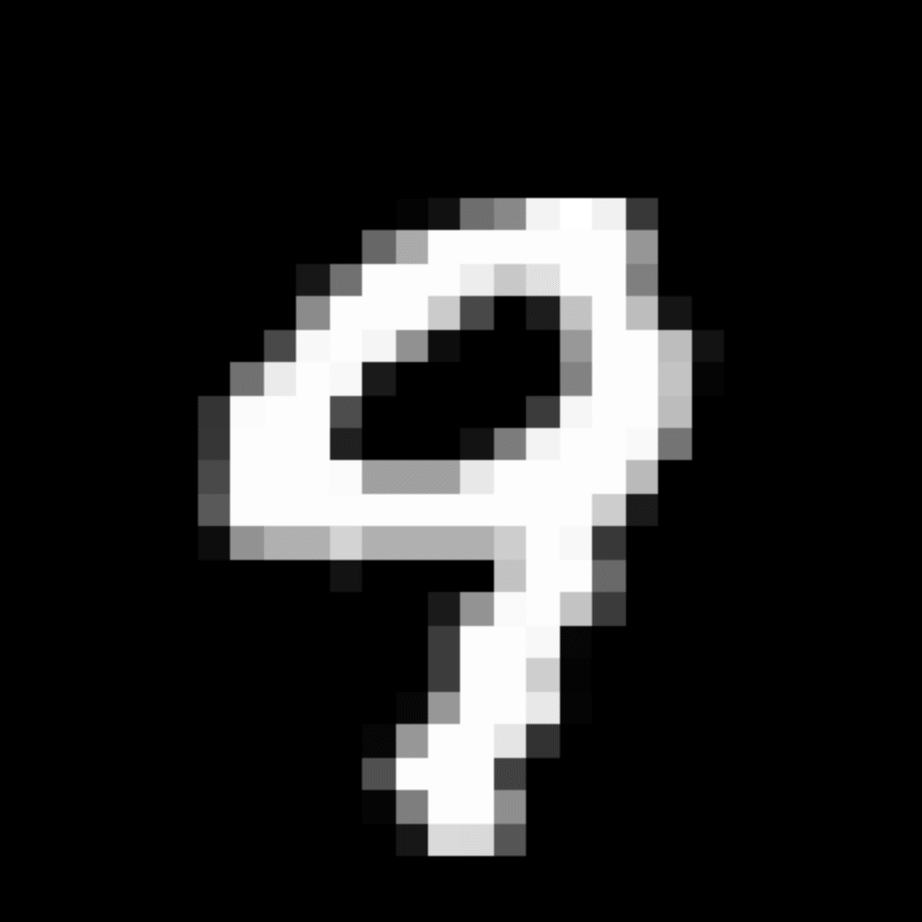
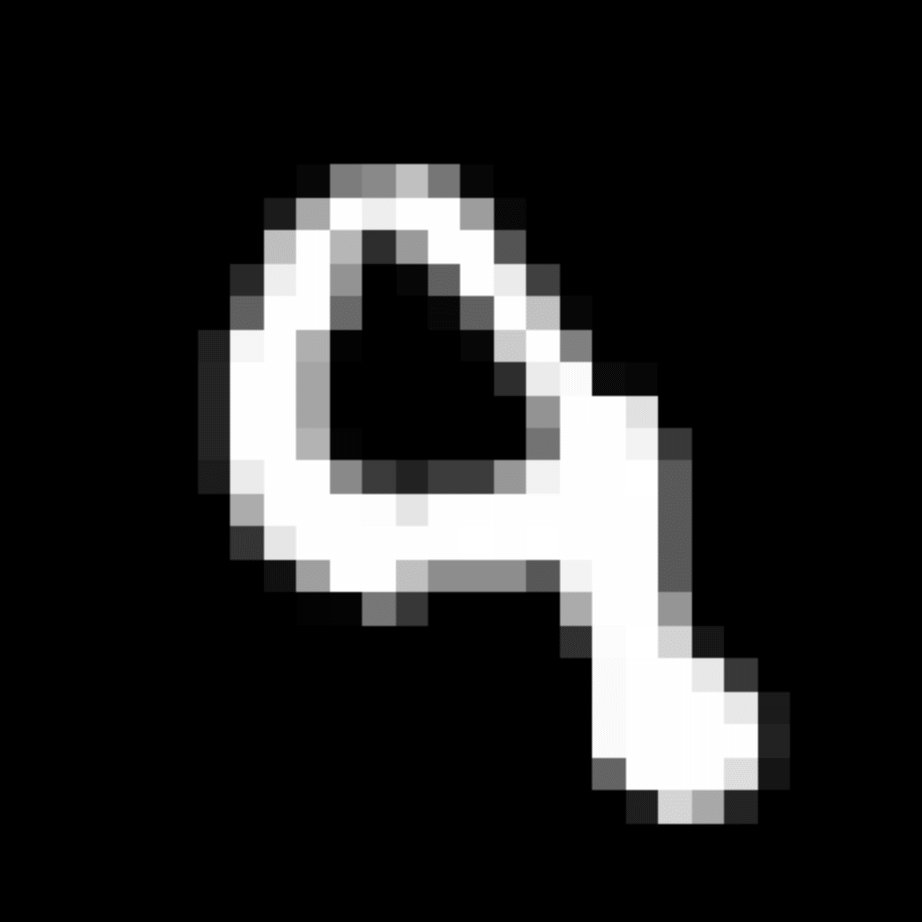
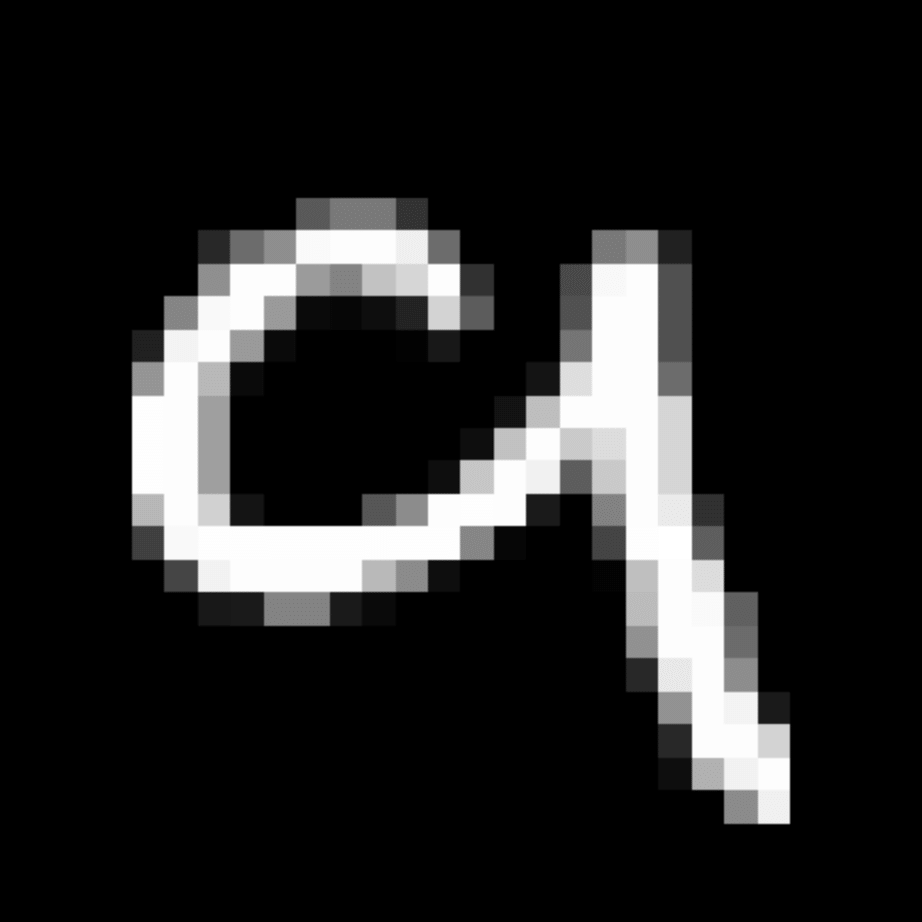
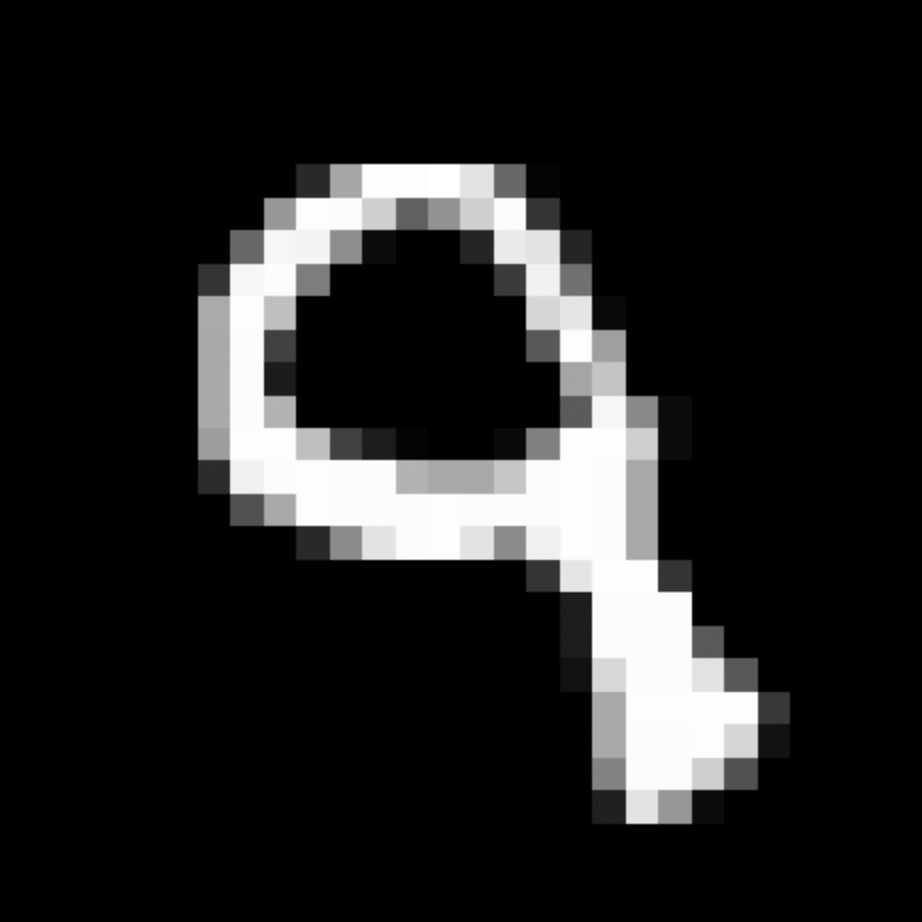
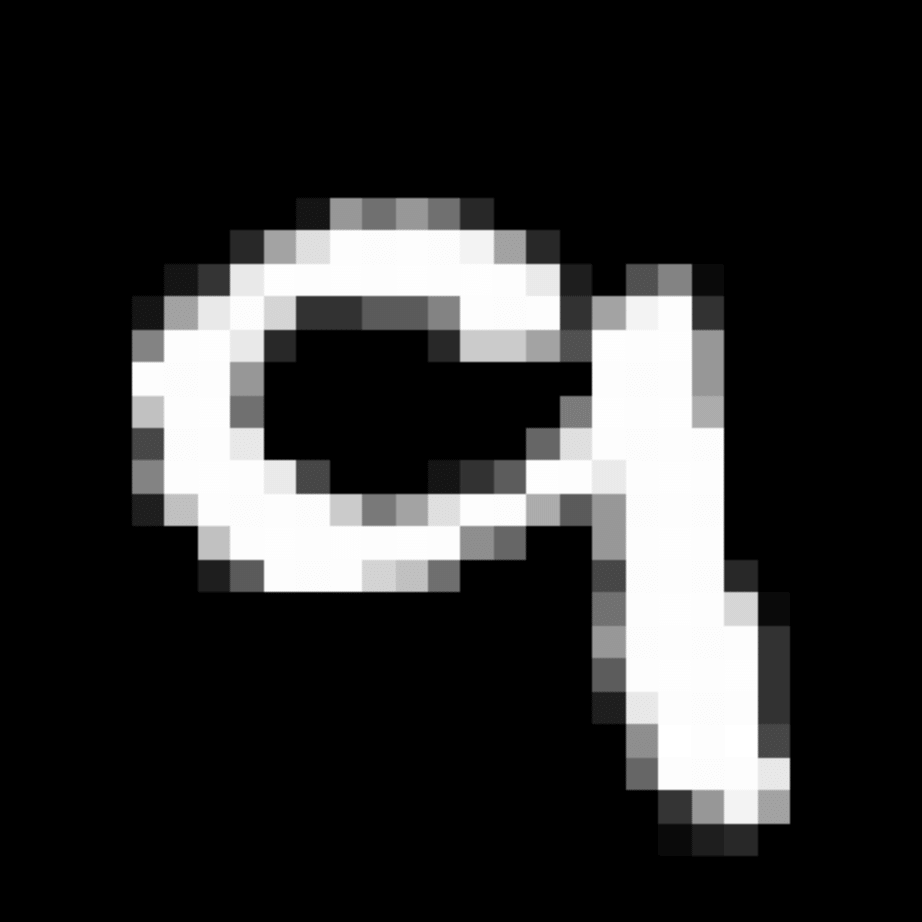
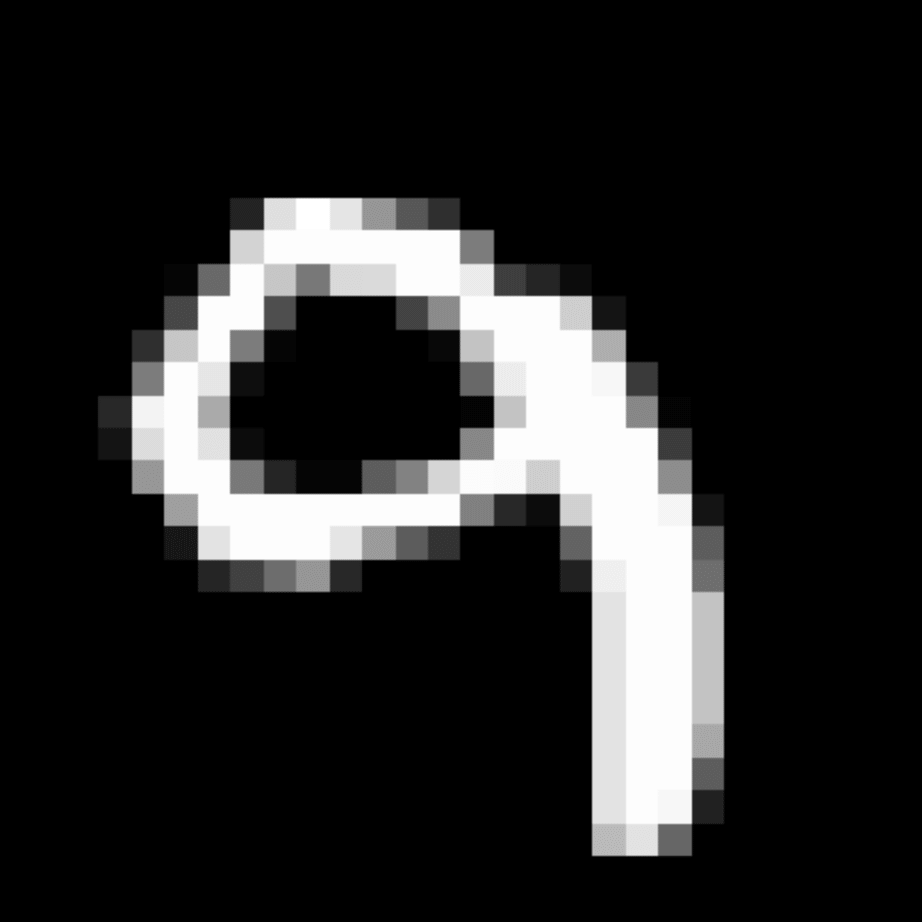
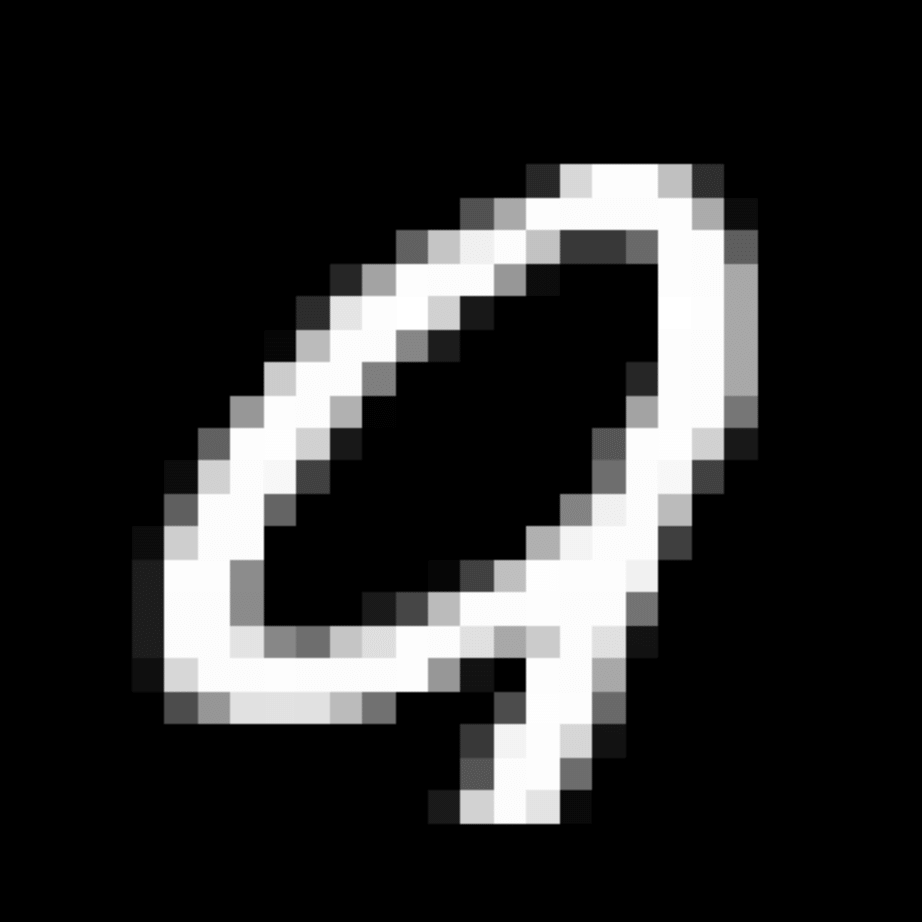
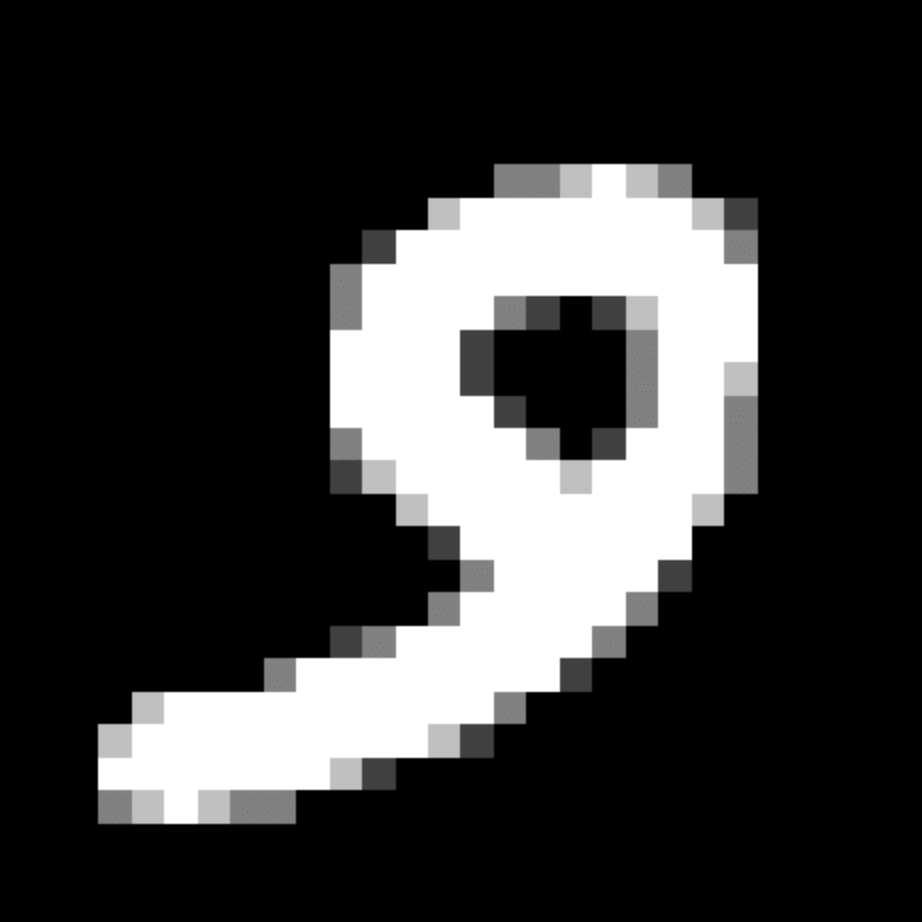
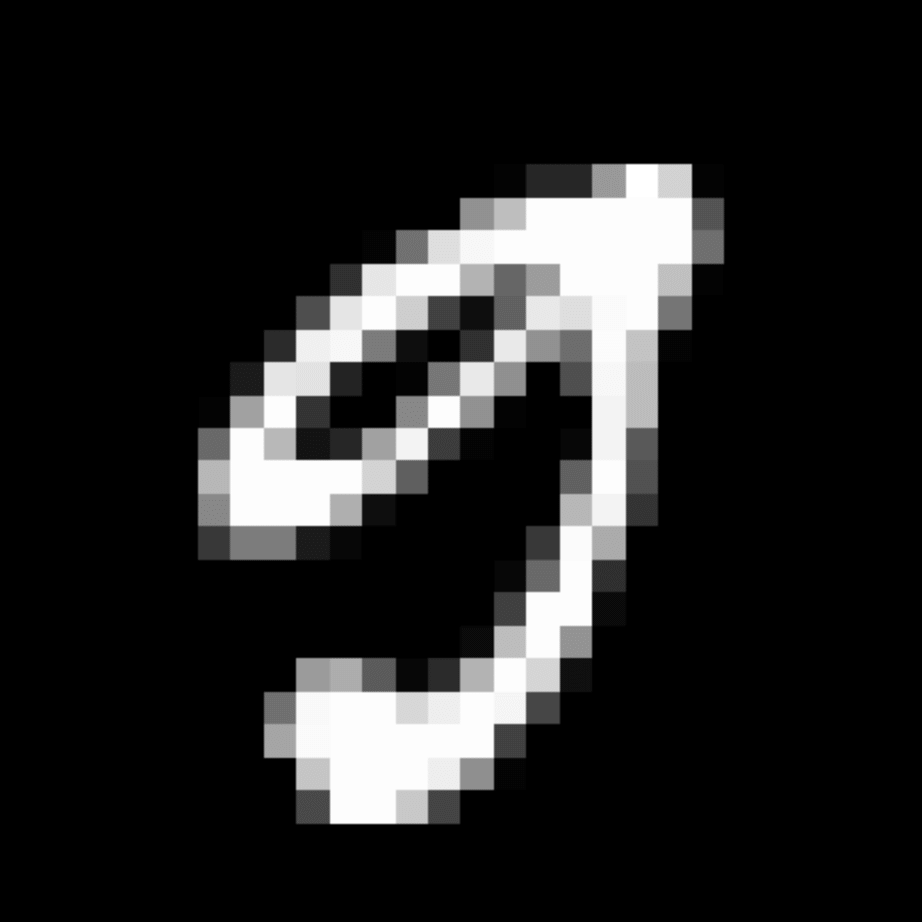
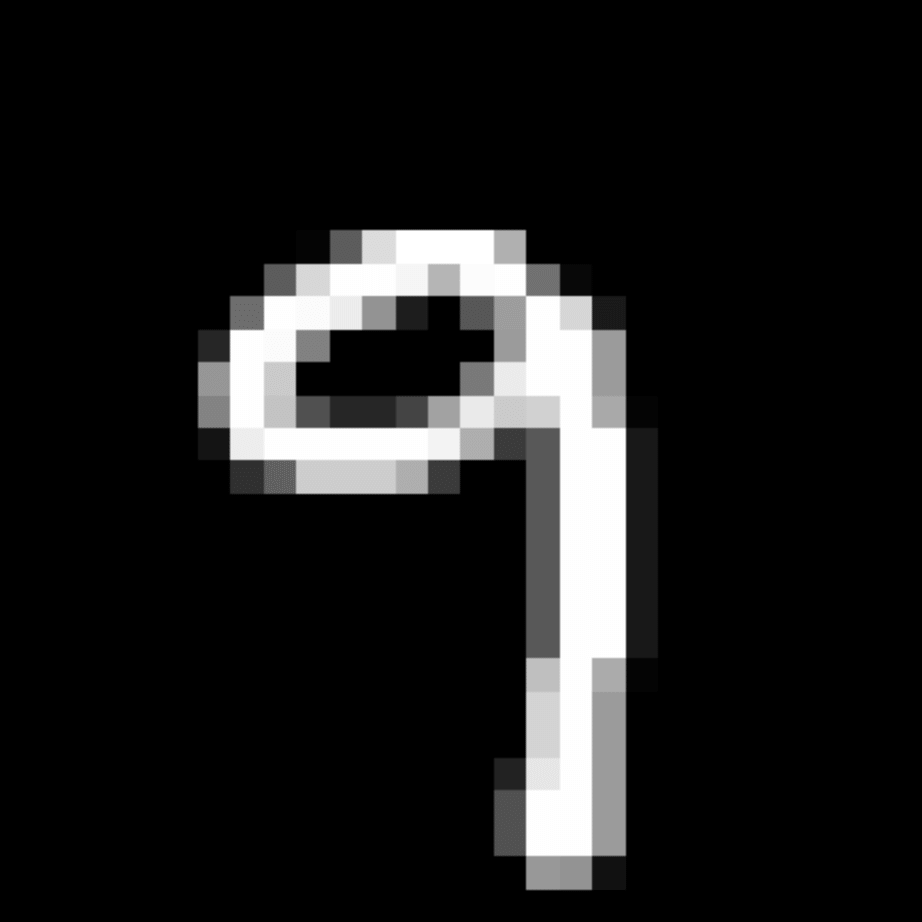
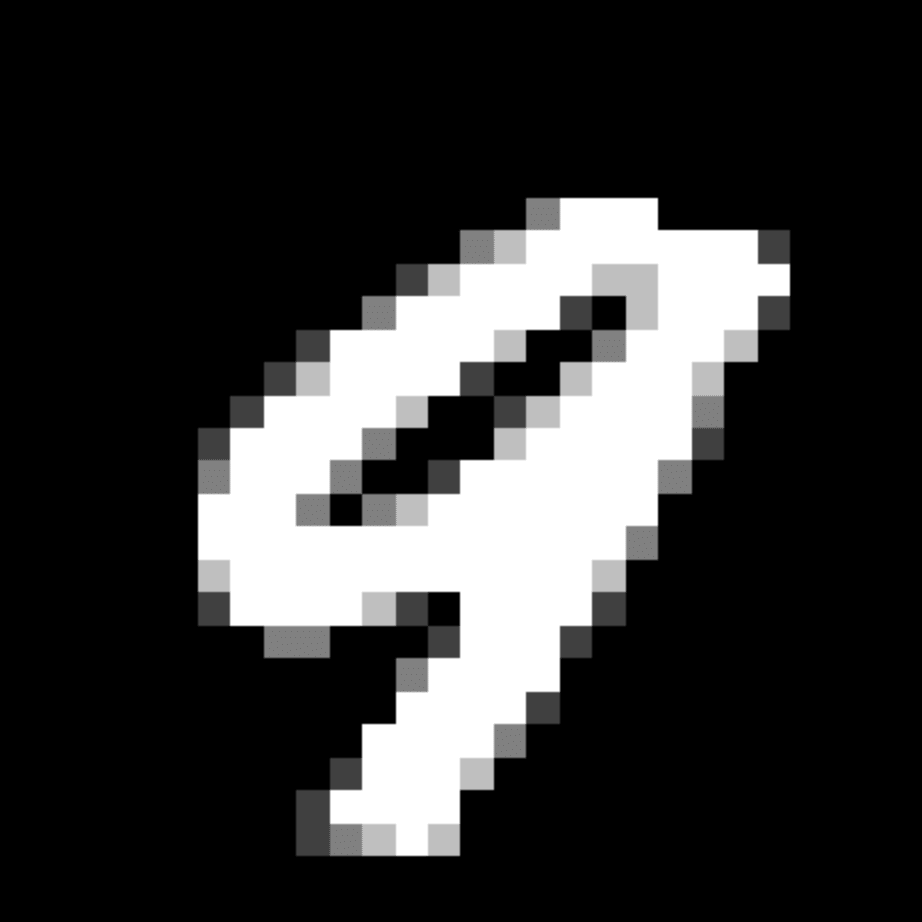
Visualisation of 5 test examples with the highest prediction probability, for each of 3 auxiliary classes, for different primary classes.
To our initial surprise, only part of the generated auxiliary labels visualised in MNIST show human-understandable knowledge. We can observe that the auxiliary classes #1 and #2 of digit nine are clustered by the direction of the "tail", and auxiliary classes #2 and #3 of digit seven are clustered by the distinction of the "horizontal line". But in most cases, there are no obvious similarities within each auxiliary class in terms of shape, colour, style, structure or semantic meaning, particularly in CIFAR-100 (which we ignored in visualisation). However, this makes more sense when we re-consider the role of the label-generation network, which is to assign auxiliary labels which assist the primary task, rather than grouping images in terms of semantic or visual similarity. The label-generation network would therefore be more effective if it were to group images in terms of a shared aspect of reasoning which the primary task is currently struggling to learn, which may not be human interpretable.
In this paper, we have presented Meta AuXiliary Learning (MAXL) for generating optimal auxiliary labels which, when trained alongside a primary task in a multi-task setup, improve the performance of the primary task. Rather than employing domain knowledge and human-defined auxiliary tasks as is typically required, MAXL is self-supervised and, combined with its general nature, has the potential to automate the process of generalisation to new levels.
The general nature of MAXL also opens up questions about how self-supervised auxiliary learning may be used to learn generic auxiliary tasks, beyond sub-class image classification. During our experiments, we also ran preliminary experiments on predicting arbitrary vectors such that the auxiliary task becomes a regression, but results so far have been inconclusive. However, the ability of MAXL to potentially learn flexible auxiliary tasks which can automatically be tuned for the primary task, now offers an exciting direction towards automated generalisation across a wide range of more complex tasks. MAXL has inspired some interesting recent works such as in knowledge transfer, differentiable data selection, and image deblurring.
If you found this work is useful in your own research, please considering citing the following.
@inproceedings{liu2019maxl,
title={Self-supervised generalisation with meta auxiliary learning},
author={Liu, Shikun and Davison, Andrew J and Johns, Edward},
booktitle={Proceedings of the 33rd International Conference on Neural Information Processing Systems},
pages={1679--1689},
year={2019}
}